
(2)已知|x|<1,|y|<1,求證: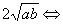 ≤1.
≤1.
(1)證明:|ax+![]() |≥
|≥![]() |ax+
|ax+![]() |2≥4ab,而|ax+
|2≥4ab,而|ax+![]() |2=a2x2+
|2=a2x2+![]() +2ab≥
+2ab≥![]() +2ab=4ab,
+2ab=4ab,
∴|ax+![]() |≥
|≥![]() .
.
(2)證法一:∵|x|<1,|y|<1,
∴1-x2>0,1-y2>0,1-xy>0.
于是要證原不等式成立,只要![]() ≤1,即證(1-x2)(1-y2)≤(1-xy)2.
≤1,即證(1-x2)(1-y2)≤(1-xy)2.
由1-x2-y2+x2y2≤1-2xy+x2y2,x2+y2≥2xy.
而該式顯然成立,故原不等式成立.
證法二:∵|x|<1,|y|<1,
∴可設x=cosα(α≠kπ,k∈Z),y=cosβ(β≠kπ,k∈Z).
于是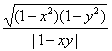 =
=![]() .
.
又∵cosαcosβ+sinαsinβ=cos(α-β)≤1,cosαcosβ-sinαsinβ=cos(α+β)≤1,
∴cosαcosβ+|sinαsinβ|≤1.
∴![]() ≤1,即
≤1,即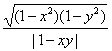 ≤1.
≤1.


科目:高中數學 來源: 題型:
| x2 |
| a |
| y2 |
| b |
| (x+y)2 |
| a+b |
| 1 |
| 2x |
| 9 |
| 1-2x |
| 1 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com