
(本題滿分12分,第Ⅰ小題4分,第Ⅱ小題5分,第Ⅲ小題3分)
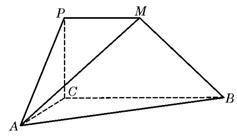 如圖,
如圖,![]() 是直角梯形,∠
是直角梯形,∠![]() =90°,
=90°,![]() ∥
∥![]() ,
,![]() =1,
=1,![]() =2,又
=2,又![]() =1,∠
=1,∠![]() =120°,
=120°,![]() ⊥
⊥![]() ,直線
,直線![]() 與直線
與直線![]() 所成的角為60°.
所成的角為60°.
(Ⅰ)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求三棱錐![]() 的體積.
的體積.
(Ⅰ)略 (Ⅱ) ![]() (Ⅲ)
(Ⅲ)![]()
解法一:
(Ⅰ)∵![]()
∴![]() ,又∵
,又∵![]() ∴
∴![]() …(4分)
…(4分)
(Ⅱ)取![]() 的中點
的中點![]() ,則
,則![]() ,連結
,連結![]() ,
,
∵![]() ,∴
,∴![]() ,從而
,從而![]()
作![]() ,交
,交![]() 的延長線于
的延長線于![]() ,連結
,連結![]() ,則由三垂線定理知,
,則由三垂線定理知,![]() ,
,
從而![]() 為二面角
為二面角![]() 的平面角
的平面角
直線![]() 與直線
與直線![]() 所成的角為
所成的角為![]() ∴
∴![]()
在![]() 中,由余弦定理得
中,由余弦定理得![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
在![]() 中,
中,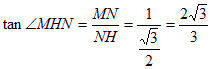
故二面角![]() 的平面角大小為
的平面角大小為![]() …(9分)
…(9分)
(Ⅲ)由(Ⅱ)知,![]() 為正方形
為正方形
∴![]() ……(12分)
……(12分)
解法二:(Ⅰ)同解法一…(4分)
(Ⅱ)在平面![]() 內,過
內,過![]() 作
作![]() ,建立空間直角坐標系
,建立空間直角坐標系![]() (如圖)
(如圖)
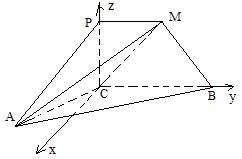 由題意有
由題意有![]() ,設
,設![]() ,
,
則![]()
由直線![]() 與直線
與直線![]() 所成的解為
所成的解為![]() ,得
,得
![]() ,即
,即![]() ,解得
,解得![]()
∴![]() ,設平面
,設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則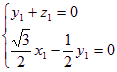 ,取
,取![]() ,得
,得![]()
平面![]() 的法向量取為
的法向量取為![]() ,設
,設![]() 與
與![]() 所成的角為
所成的角為![]() ,則
,則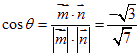
顯然,二面角![]() 的平面角為銳角,故二面角
的平面角為銳角,故二面角![]() 的平面角大小為
的平面角大小為![]()
(Ⅲ)取平面![]() 的法向量取為
的法向量取為![]() ,則點A到平面
,則點A到平面![]() 的距離
的距離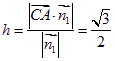
∵![]() ,∴
,∴![]() …(12分)
…(12分)


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數學 來源: 題型:
(本題滿分12分,第(1)小題5分,第(2)小題7分)
已知銳角△ABC中,三個內角為A、B、C,向量![]() =
=![]() 2-2
2-2![]() ,
,![]() +
+![]()
![]() ,
,![]() =
=![]()
![]() -
-![]() ,1+
,1+![]()
![]() ,
,![]() ∥
∥![]() .
.
(1)求∠A的大小;
(2)求函數![]() =2
=2![]() +
+![]() 取得最大值時,∠B的大小.
取得最大值時,∠B的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分12分,第(1)小題6分,第(2)小題6分)
如圖,![]() 是圓柱體
是圓柱體![]() 的一條母線,
的一條母線,![]() 過底面圓的圓心
過底面圓的圓心 ![]() ,
,![]() 是圓
是圓![]() 上不與點
上不與點![]() 、
、![]() 重合的任意一點,已知棱
重合的任意一點,已知棱![]() ,
, ![]() ,
,![]() .
.
(1)求直線![]() 與平面
與平面![]() 所成的角的大小;
所成的角的大小;
(2)將四面體![]() 繞母線
繞母線![]() 轉動一周,求
轉動一周,求![]() 的三邊在旋 轉過程中所圍成的幾何體的體積.
的三邊在旋 轉過程中所圍成的幾何體的體積.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年上海市高三上學期期中考試數學卷 題型:解答題
(本題滿分12分,第1小題6分,第小題6分)
設函數 的定義域為集合A,函數
的定義域為集合A,函數 的定義域為集合B。
的定義域為集合B。
(1)求A∩B;
(2)若 ,求實數
,求實數 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源:2010年上海市高二第二學期階段質量檢測數學試題 題型:解答題
(本題滿分12分,第(1)小題6分,第(2)小題6分)
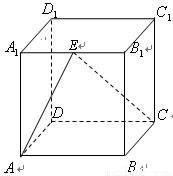
如圖,在棱長為1的正方體中,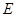 是棱
是棱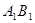 的中點,
的中點,
(1)求證: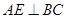 ;
;
(2)求 與平面
與平面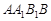 所成角大小(用反三角函數表示).
所成角大小(用反三角函數表示).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com