
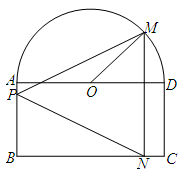
如圖所示,一個(gè)半圓和長(zhǎng)方形組成的鐵皮,長(zhǎng)方形的邊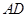 為半圓的直徑,
為半圓的直徑,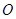 為半圓的圓心,
為半圓的圓心, ,
,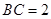 ,現(xiàn)要將此鐵皮剪出一個(gè)等腰三角形
,現(xiàn)要將此鐵皮剪出一個(gè)等腰三角形 ,其底邊
,其底邊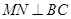 .
.
(1)設(shè)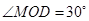 ,求三角形鐵皮
,求三角形鐵皮 的面積;
的面積;
(2)求剪下的鐵皮三角形 的面積的最大值.
的面積的最大值.
(1)三角形鐵皮 的面積為
的面積為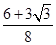 ;(2)剪下的鐵皮三角形
;(2)剪下的鐵皮三角形 的面積的最大值為
的面積的最大值為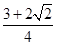 .
.
解析試題分析:(1)利用銳角三角函數(shù)求出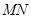 和
和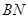 的長(zhǎng)度,然后以
的長(zhǎng)度,然后以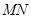 為底邊、以
為底邊、以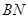 為高,利用三角形面積公式求出三角形
為高,利用三角形面積公式求出三角形 的面積;(2)設(shè)
的面積;(2)設(shè)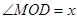 ,以銳角
,以銳角 為自變量將
為自變量將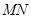 和
和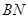 的長(zhǎng)度表示出來(lái),并利用面積公式求出三角形
的長(zhǎng)度表示出來(lái),并利用面積公式求出三角形 的面積的表達(dá)式
的面積的表達(dá)式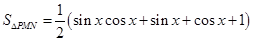 ,利用
,利用 與
與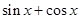 之間的關(guān)系
之間的關(guān)系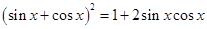 ,令
,令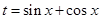 將三角形
將三角形 的面積的表達(dá)式表示為以
的面積的表達(dá)式表示為以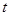 為自變量的二次函數(shù),利用二次函數(shù)的單調(diào)性求出三角形
為自變量的二次函數(shù),利用二次函數(shù)的單調(diào)性求出三角形 的面積的最大值,但是要注意自變量
的面積的最大值,但是要注意自變量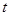 的取值范圍作為新函數(shù)的定義域.
的取值范圍作為新函數(shù)的定義域.
試題解析:(1)由題意知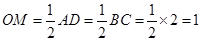 ,
,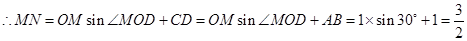 ,
,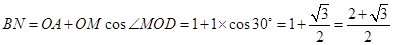 ,
,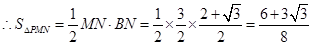 ,即三角形鐵皮
,即三角形鐵皮 的面積為
的面積為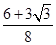 ;
;
(2)設(shè)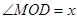 ,則
,則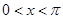 ,
,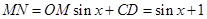 ,
,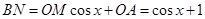 ,
,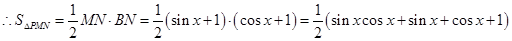 ,
,
令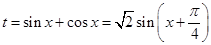 ,由于
,由于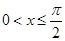 ,所以
,所以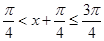 ,
,
則有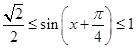 ,所以
,所以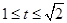 ,
,
且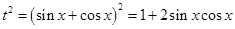 ,所以
,所以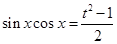 ,
,
故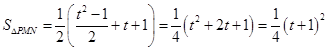 ,
,
而函數(shù)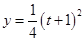 在區(qū)間
在區(qū)間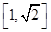 上單調(diào)遞增,
上單調(diào)遞增,
故當(dāng)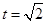 時(shí),
時(shí),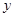 取最大值,即
取最大值,即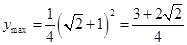 ,
,
即剪下的鐵皮三角形 的面積的最大值為
的面積的最大值為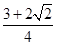 .
.
考點(diǎn):1.三角形的面積;2.三角函數(shù)的最值;3.二次函數(shù)的最值


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
張林在李明的農(nóng)場(chǎng)附近建了一個(gè)小型工廠,由于工廠生產(chǎn)須占用農(nóng)場(chǎng)的部分資源,因此李明每年向張林索賠以彌補(bǔ)經(jīng)濟(jì)損失并獲得一定凈收入.工廠在不賠付農(nóng)場(chǎng)的情況下,工廠的年利潤(rùn)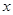 (元)與年產(chǎn)量
(元)與年產(chǎn)量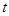 (噸)滿足函數(shù)關(guān)系
(噸)滿足函數(shù)關(guān)系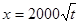 .若工廠每生產(chǎn)一噸產(chǎn)品必須賠付農(nóng)場(chǎng)
.若工廠每生產(chǎn)一噸產(chǎn)品必須賠付農(nóng)場(chǎng)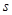 元(以下稱
元(以下稱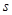 為賠付價(jià)格).
為賠付價(jià)格).
(Ⅰ)將工廠的年利潤(rùn)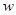 (元)表示為年產(chǎn)量
(元)表示為年產(chǎn)量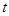 (噸)的函數(shù),并求出工廠獲得最大利潤(rùn)的年產(chǎn)量;
(噸)的函數(shù),并求出工廠獲得最大利潤(rùn)的年產(chǎn)量;
(Ⅱ)若農(nóng)場(chǎng)每年受工廠生產(chǎn)影響的經(jīng)濟(jì)損失金額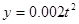 (元),在工廠按照獲得最大利潤(rùn)的產(chǎn)量進(jìn)行生產(chǎn)的前提下,農(nóng)場(chǎng)要在索賠中獲得最大凈收入,應(yīng)向張林的工廠要求賠付價(jià)格
(元),在工廠按照獲得最大利潤(rùn)的產(chǎn)量進(jìn)行生產(chǎn)的前提下,農(nóng)場(chǎng)要在索賠中獲得最大凈收入,應(yīng)向張林的工廠要求賠付價(jià)格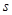 是多少?
是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知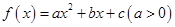 ,當(dāng)
,當(dāng)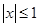 時(shí),
時(shí),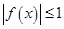 .
.
(1)證明: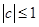 ;
;
(2)若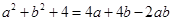 成立,請(qǐng)先求出
成立,請(qǐng)先求出 的值,并利用
的值,并利用 值的特點(diǎn)求出函數(shù)
值的特點(diǎn)求出函數(shù) 的表達(dá)式.
的表達(dá)式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)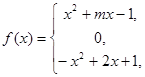
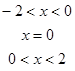 是奇函數(shù).
是奇函數(shù).
(1)求實(shí)數(shù) 的值;
的值;
(2)若函數(shù) 在區(qū)間
在區(qū)間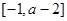 上單調(diào)遞增,求實(shí)數(shù)
上單調(diào)遞增,求實(shí)數(shù)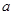 的取值范圍;
的取值范圍;
(3)求函數(shù) 的值域.
的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)
(Ⅰ)若 在
在 上為增函數(shù),求實(shí)數(shù)
上為增函數(shù),求實(shí)數(shù) 的取值范圍;
的取值范圍;
(Ⅱ)當(dāng) 時(shí),方程
時(shí),方程 有實(shí)根,求實(shí)數(shù)
有實(shí)根,求實(shí)數(shù) 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知某公司生產(chǎn)品牌服裝的年固定成本是10萬(wàn)元,每生產(chǎn)千件,須另投入2 7萬(wàn)元,設(shè)該公司年內(nèi)共生產(chǎn)該品牌服裝x千件并全部銷售完,每千件的銷售收入為R(x)萬(wàn)元,且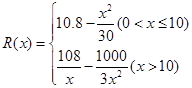
(1)寫出年利潤(rùn)W(萬(wàn)元)關(guān)于年產(chǎn)量x(千件)的函數(shù)解析式;
(2)年產(chǎn)量為多少千件時(shí),該公司在這一品牌服裝的生產(chǎn)中所獲利潤(rùn)最大?(注:年利潤(rùn)=年銷售收入 年總成本)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知一家公司生產(chǎn)某種產(chǎn)品的年固定成本為10萬(wàn)元,每生產(chǎn)1千件該產(chǎn)品需另投入2.7萬(wàn)元,設(shè)該公司一年內(nèi)生產(chǎn)該產(chǎn)品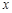 千件并全部銷售完,每千件的銷售收入為
千件并全部銷售完,每千件的銷售收入為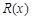 萬(wàn)元,且
萬(wàn)元,且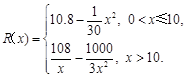
(Ⅰ)寫出年利潤(rùn)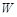 (萬(wàn)元)關(guān)于年產(chǎn)量
(萬(wàn)元)關(guān)于年產(chǎn)量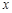 (千件)的函數(shù)解析式;
(千件)的函數(shù)解析式;
(Ⅱ)年產(chǎn)量為多少千件時(shí),該公司在這一產(chǎn)品的產(chǎn)銷過(guò)程中所獲利潤(rùn)最大.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)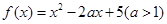 .
.
(1)若函數(shù) 的定義域和值域均為
的定義域和值域均為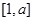 ,求實(shí)數(shù)
,求實(shí)數(shù) 的值;
的值;
(2)若 在區(qū)間
在區(qū)間 上是減函數(shù),且對(duì)任意的
上是減函數(shù),且對(duì)任意的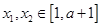 ,總有
,總有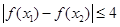 ,求實(shí)數(shù)
,求實(shí)數(shù) 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
設(shè)
(1)當(dāng) ,求
,求 的取值范圍;
的取值范圍;
(2)若對(duì)任意 ,
, 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù) 的最小值.
的最小值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com