中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情
設A={x∈R|x2+4x-5=0},B={x∈R|x2+2ax-2a2+3=0,a∈R},

(1)若A∩B=B,求實數a的范圍;

(2)若A∩B=A,求實數a的值.

解：(1)由已知得A={-5,1},∵A∩B=B,∴BA.則B可能有,{-5},{1},{-5,1}四種情況.

①當B=時,方程x2+2ax-2a2+3=0無實數解,

∴Δ=4a2-4(-2a2+3)=12(a2-1)＜0,即-1＜a＜1.

②當B={-5}時,Δ=0且(-5)2+2a(-5)-2a2+3=0,a無解,即B≠{-5}.

③當B={1}時,Δ=0且12+2a-2a2+3=0,解得a=-1.

④當B={-5,1}時,由根與系數的關系有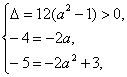解得a=2,

綜上可得-1≤a＜1或a=2.

(2)∵A∩B=A,∴AB,

即{-5,1}B.∴B={-5,1}.

由(1)知a=2,即當A∩B=A時,a=2.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

設A={x∈R||2x-x2|≤x}，B={x∈R||
x
1-x
|≤
x
1-x
}，C={x∈R|ax2+x+b＜0}，若（A∪B）∩C=∅，（A∪B）∪C=R，求a，b的值．

查看答案和解析>>

科目：高中數學 來源： 題型：

設集合A={x∈R|x2-4x=0}，集合B={x∈R|x2-2（a+1）x+a2-1=0}，
（1）若B=∅，求實數a的取值范圍；
（2）若B≠∅，且A∩B=B，求實數a的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

有以下4個命題：
①A={x∈R|x2+1=0}，B={x∈R|4＜x＜3}，則A=B．
②已知函數f（x）是偶函數，而且在（0，+∞）上增函數，則在（-∞，0）上也是增函數．；
③函數f（x）=x2-（k2+3k+9）x+2（k是實常數）在區間（-∞，-2010）是減函數．
④設f(x)=
ex-e-x
2
，g(x)=
ex+e-x
2
，則g(2x)=[f(x)]2+[g(x)]2．
其中正確的命題序號是
③④
③④
．

查看答案和解析>>

科目：高中數學 來源： 題型：

設全集U=R，集合A={x∈R|x2-7x+6＜0}，集合B={x∈R|-1≤x＜3}．求A∩B，A∪B，A∩（?UB）．

查看答案和解析>>

同步練習冊答案