Question

求下列各題中f（x）的解析式：

（1）已知函數f（x+1）=x²-3x+2，求f（x）；

（2）已知f（+4）=x+8，求f（x²）；

（3）已知函數y=f（x），滿足2f（x）+f（）=2x，x∈R且x≠0，求f（x）；

（4）已知一次函數f（x）滿足f［f（x）］=4x-1，求f（x）.

Answer 1

解析：求函數的解析式關鍵在于弄清對于“x”而言，“f”是怎樣的對應法則，至于選擇什么符號表示自變量沒有關系.（1）把x+1看成整體，利用換元法可以求出原來的函數f（x）；（2）利用配方法或換元法；（3）對于較復雜的函數解析式，如函數y=f（x），滿足2f（x）+f（）=2x，x∈R且x≠0.如果我們將f（x）、f（）看作是整體，則本題可轉化為一個關于f（x）、f（）的方程問題；(4)由于已知f（x）是一次函數，因此可設f（x）=ax+b（a≠0），利用待定系數法求出a,b.

解：（1）令t=x+1，則x=t-1，代入得f（t）=（t-1）²-3（t-1）+2，

∴f（t）=t²-5t+6，即f（x）=x²-5x+6.

    也可以用配方法.

∵f（x+1）=x²-3x+2=（x+1）²-5x+1=（x+1）²-5（x+1）+6，

∴f（x）=x²-5x+6.

（2）解法一：∵f（+4）=x+8=（+4）²-16，

∴f（x）=x²-16（x≥4）.∴f（x²）=x⁴-16（x≤-2或x≥2）.

解法二：設+4=t≥4，則=t-4，x=（t-4）²，

∴f（t）=（t-4）²+8（t-4）=t²-16.∴f（x）=x²-16（x≥4）.

∴f（x²）=x⁴-16（x≤-2或x≥2）.

（3）由2f（x）+f（）=2x                                ①

    將x換成，則換成x，得

2f（）+f（x）=                                          ②

①×2-②，得3f（x）=4x-，即f（x）=-.

（4）因為f（x）是一次函數，設f（x）=ax+b（a≠0），

    則f［f（x）］=f（ax+b）=a（ax+b）+b=a²x+ab+b=4x-1.

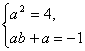
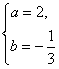∴或

∴f（x）=2x-或f（x）=-2x+1.