
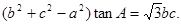
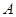 ;
;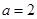 ,求
,求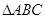 面積S的最大值.
面積S的最大值.科目:高中數學 來源:不詳 題型:解答題
 ),現有可供建造第三面圍墻的材料60米(兩面墻的長均大于60米),為了使得小老虎能健康成長,要求所建造的三角形露天活動室盡可能大,記
),現有可供建造第三面圍墻的材料60米(兩面墻的長均大于60米),為了使得小老虎能健康成長,要求所建造的三角形露天活動室盡可能大,記 ,
,
 為多少時,所建造的三角形露天活動室的面積最大?
為多少時,所建造的三角形露天活動室的面積最大?查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
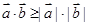 ,則存在正實數
,則存在正實數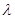 ,使得
,使得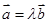 ;③若函數
;③若函數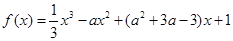 在點
在點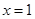 處取得極值,則實數
處取得極值,則實數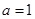 或
或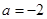 ;④函數
;④函數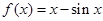 有且只有一個零點.其中正確命題的序號是 .
有且只有一個零點.其中正確命題的序號是 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com