
 .
. 的單調遞減區間;
的單調遞減區間; 的圖像向左平移
的圖像向左平移 個單位,再將得到的圖像橫坐標變為原來的2倍(縱坐標不變)后得到
個單位,再將得到的圖像橫坐標變為原來的2倍(縱坐標不變)后得到 的圖像,若
的圖像,若 的圖像與直線
的圖像與直線 交點的橫坐標由小到大依次是
交點的橫坐標由小到大依次是 求數列
求數列 的前2n項的和。
的前2n項的和。 的單調遞減區間為
的單調遞減區間為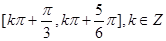 ;(Ⅱ)
;(Ⅱ)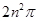 .
. 的單調遞減區間,首先對
的單調遞減區間,首先對 進行恒等變化,將它變為一個角的一個三角函數,然后利用三角函數的單調性,來求函數
進行恒等變化,將它變為一個角的一個三角函數,然后利用三角函數的單調性,來求函數 的單調遞減區間,本題首先通過降冪公式降冪,及倍角公式,得到
的單調遞減區間,本題首先通過降冪公式降冪,及倍角公式,得到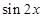 與
與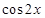 的關系式,再利用兩角和的三角函數公式,得到
的關系式,再利用兩角和的三角函數公式,得到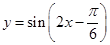 ,從而得到單調遞減區間;(Ⅱ)本題由
,從而得到單調遞減區間;(Ⅱ)本題由 的圖像,根據圖象的變化規律得到函數
的圖像,根據圖象的變化規律得到函數 的圖象;從而求出
的圖象;從而求出 的解析式,再結合正弦曲線的對稱性,周期性求出相鄰兩項的和及其規律,最后結合等差數列的求和公式即可得到結論.
的解析式,再結合正弦曲線的對稱性,周期性求出相鄰兩項的和及其規律,最后結合等差數列的求和公式即可得到結論.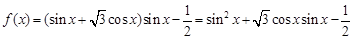
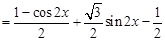
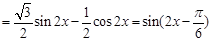 . 4分
. 4分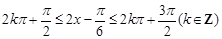 ,所以
,所以
 的單調遞減區間為
的單調遞減區間為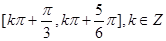 . 6分
. 6分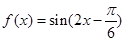 的圖象向左平移
的圖象向左平移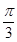 個單位后,
個單位后,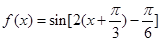
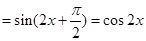 . 7分
. 7分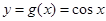 , 8分解法一:若函數
, 8分解法一:若函數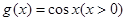 的圖象與直線
的圖象與直線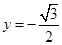 交點的橫坐標由小到大依次是
交點的橫坐標由小到大依次是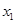 、
、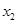 、
、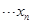 、
、 、
、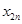 ,則由余弦曲線的對稱性,周期性可知,
,則由余弦曲線的對稱性,周期性可知,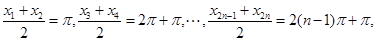 9分
9分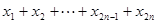

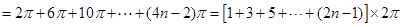
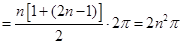 . 12分
. 12分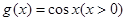 的圖象與直線
的圖象與直線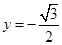 交點的橫坐標由小到大依次是
交點的橫坐標由小到大依次是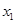 、
、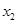 、
、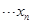 、
、 、
、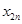 ,則
,則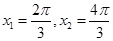 . 9分
. 9分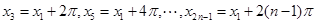 ;
;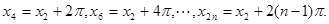
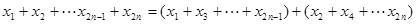
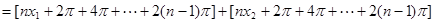
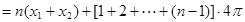
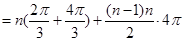
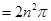 . 12分
. 12分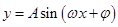 的圖象變換.
的圖象變換.

 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源:不詳 題型:填空題
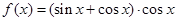 ,給出下列命題:
,給出下列命題: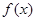 的最小正周期為
的最小正周期為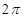 ;
;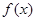 在區間
在區間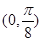 上為增函數;
上為增函數;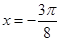 是函數
是函數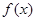 圖像的一條對稱軸;
圖像的一條對稱軸;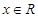 ,恒有
,恒有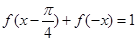 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com