(文)定義在R上函數f(x)對任意實數x、y∈R都有f(x+y)=f(x)•f(y),且當x<0時,f(x)>1.
(1)證明當x>0時,0<f(x)<1;
(2)判斷函數f(x)的單調性并證明;
(3)如果對任意實數x、y有f(x2)•f(y2)≤f(axy)恒成立,求實數a的取值范圍.
【答案】
分析:(1)令x=0,y=-1,可求得f (0)=1,再令x>0得-x<0,利用已知當x<0時,f(x)>1即可證得x>0時,0<f(x)<1;
(2)設x
1、x
2∈(-∞,+∞),且x
1<x
2,作差f (x
2)-f (x
1)=f[x
1+(x
2-x
1)]-f (x
1)=[f (x
2-x
1)-1]f (x
1)結合題意,判斷其符號即可;
(3)依題意,f(x
2)•f(y
2)≤f(axy)恒成立,函數f(x)為減函數?x
2+y
2≥axy 對任意實數x、y恒成立?|a|≤|
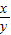
|+|
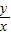
|對任意實數x、y恒成立,由基本不等式即可求實數a的取值范圍.
解答:證明:(1)令x=0,y=-1則f (0-1)=f (0)•f (-1)(∵f (-1)≠0)⇒f (0)=1 …(2分)
當 x<0時,f (x)>1>0,
當 x>0時,-x<0
∴f (-x)>1>0,又f (0)=f (-x)•f (x)=1,
∴0<f (x)=
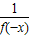
<1,即對任意x>0,恒有0<f (x)<1 …(5分)
(2)f (x)在R上是減函數 …(7分)
證明:設x
1、x
2∈(-∞,+∞),且x
1<x
2;
f (x
2)-f (x
1)=f[x
1+(x
2-x
1)]-f (x
1)
=f (x
2-x
1)•f (x
1)-f (x
1)=[f (x
2-x
1)-1]f (x
1),
∵x
2-x
1>0,
∴f (x
2-x
1)<1,
∴f (x
2)-f (x
1)<0,
∴[f (x
2-x
1)-1]f (x
1)<0,
∴f (x)在(-∞,+∞)上是減函數. …(10分)
(3)∵f (x
2)•f (y
2)=f (x
2+y
2)≤f (axy),
∴x
2+y
2≥axy 對任意實數x、y恒成立,
即x
2+y
2≥|axy|=|a||x||y|對任意實數x、y恒成立,
∴|a|≤|
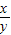
|+|
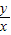
|對任意實數x、y恒成立,
∴|a|≤2,即-2≤a≤2為所求.…(14分)
點評:本題考查抽象函數的應用,考查函數的單調性的判斷與證明,突出考查等價轉化思想的運用,考查基本不等式,綜合性強,難度大,屬于難題.

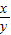 |+|
|+|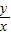 |對任意實數x、y恒成立,由基本不等式即可求實數a的取值范圍.
|對任意實數x、y恒成立,由基本不等式即可求實數a的取值范圍.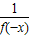 <1,即對任意x>0,恒有0<f (x)<1 …(5分)
<1,即對任意x>0,恒有0<f (x)<1 …(5分)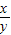 |+|
|+|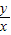 |對任意實數x、y恒成立,
|對任意實數x、y恒成立,

 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案