Question

已知定義域為R的函數f（x）=|x²-1|，若關于x的方程f²（x）+bf（x）+c=0恰有7個不同的實數解x₁，x₂，x₃，x₄，x₅，x₆，x₇，則x₁+x₂+x₃+x₄+x₅+x₆+x₇=    ．

Answer 1

【答案】分析：可令f（x）=t則關于x的方程f²（x）+bf（x）+c=0就轉化為關于t的方程t²+bt+c=0作出f（x）=|x²-1|的圖象根據圖象可得要使關于x的方程f²（x）+bf（x）+c=0恰有7個不同的實數解即使關于t的方程t²+bt+c=0有兩個不同實根且f（x）=|x²-1|的圖象與y=t的圖象的交點的橫坐標即為方程f²（x）+bf（x）+c=0的7個不同的實數解再結合f（x）=|x²-1|的圖象可知t₁=1，0＜t₂＜1故根據對稱性可得7個不同的實數解的和為0．
解答：解：令f（x）=t則關于x的方程f²（x）+bf（x）+c=0就轉化為關于t的方程t²+bt+c=0
故f（x）=|x²-1|的圖象與y=t的圖象的交點的橫坐標即為方程f²（x）+bf（x）+c=0的7個不同的實數解
所以關于t的方程t²+bt+c=0有兩個不同實
作出f（x）=|x²-1|的圖象如下圖則必有y=t在圖示的兩個位置才有關于x的方程f²（x）+bf（x）+c=0恰有7個不同的實數
解，即t₁=1，0＜t₂＜1

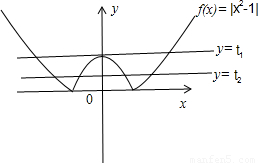
根據f（x）=|x²-1|的圖象關于y軸對稱故方程f²（x）+bf（x）+c=0的7個不同的實數解中有一個為0其余6個均關于原點對稱故x₁+x₂+x₃+x₄+x₅+x₆+x₇=0
故答案為0
點評：數形結合是數學解題中常用的思想方法，能夠變抽象思維為形象思維，有助于把握數學問題的本質；另外，由于使用了數形結合的方法，很多問題便迎刃而解，且解法簡捷．