Question

已知直線l與直線2x-y+4=0平行，且與拋物線y=x²相切，求直線l的方程．

Answer 1

【答案】分析：因為要求的直線與直線2x-y+4=0平行得到斜率相等，設出直線方程與拋物線解析式聯立，消去y得到一個一元二次方程，由直線與拋物線x²=y相切得到直線與拋物線有且只有一個交點，即方程有兩個相等的實數根，令根的判別式為0確定出直線解析式即可．
解答：解：由直線與直線2x-y+4=0平行得到斜率相等，可設直線y=2x+m，
又因為由直線與拋物線x²=y相切得到直線與拋物線有且只有一個交點，
聯立得 ，
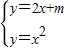
消去y得x²-2x-m=0可知方程有兩個相等的實數根即△=4+4m=0，
解得m=-1，
所以此直線方程為y=2x-1即2x-y-1=0．
故答案為2x-y-1=0．
點評：考查學生掌握兩直線平行時斜率相等，理解直線與拋物線相切時滿足的條件，以及會用待定系數法求直線一般式方程的能力．
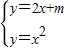