
(福建卷理22)已知函數f(x)=ln(1+x)-x1
(Ⅰ)求f(x)的單調區間;
(Ⅱ)記f(x)在區間![]() (n∈N*)上的最小值為bx令an=ln(1+n)-bx.
(n∈N*)上的最小值為bx令an=ln(1+n)-bx.
(Ⅲ)如果對一切n,不等式![]() 恒成立,求實數c的取值范圍;
恒成立,求實數c的取值范圍;
(Ⅳ)求證: ![]()
【標準答案】解法一:
(I)因為f(x)=ln(1+x)-x,所以函數定義域為(-1,+![]() ),且f〃(x)=
),且f〃(x)=![]() -1=
-1=![]() .
.
由f〃(x)>0得-1<x<0,f(x)的單調遞增區間為(-1,0);
由f〃(x)<0得x>0,f(x)的單調遞增區間為(0,+![]() ).
).
(II)因為f(x)在[0,n]上是減函數,所以bn=f(n)=ln(1+n)-n,
則an=ln(1+n)-bn=ln(1+n)-ln(1+n)+n=n.
(i)![]()
![]()
> ![]()
又lim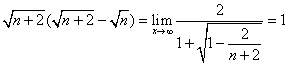 ,
,
因此c<1,即實數c的取值范圍是(-![]() ,1).
,1).
(II)由(i)知![]()

![]() N*)
N*)![]()
解法二:(Ⅰ)同解法一.
(Ⅱ)因為f(x)在![]() 上是減函數,所以
上是減函數,所以![]()
則![]()
(i)因為![]() 對n∈N*恒成立.所以
對n∈N*恒成立.所以![]() 對n∈N*恒成立.
對n∈N*恒成立.
則![]() 對n∈N*恒成立.
對n∈N*恒成立.
設![]() n∈N*,則c<g(n)對n∈N*恒成立.
n∈N*,則c<g(n)對n∈N*恒成立.
考慮![]()
因為![]() =0,
=0,
所以![]() 內是減函數;則當n∈N*時,g(n)隨n的增大而減小,
內是減函數;則當n∈N*時,g(n)隨n的增大而減小,
又因為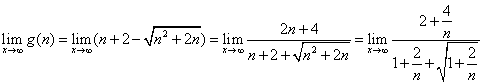 =1.
=1.
所以對一切![]() 因此c≤1,即實數c的取值范圍是(-∞,1].
因此c≤1,即實數c的取值范圍是(-∞,1].
(ⅱ) 由(ⅰ)知![]()
下面用數學歸納法證明不等式![]()
①當n=1時,左邊=![]() ,右邊=
,右邊=![]() ,左邊<右邊.不等式成立.
,左邊<右邊.不等式成立.
②假設當n=k時,不等式成立.即![]()
當n=k+1時,
![]()
=![]()
即n=k+1時,不等式成立
綜合①、②得,不等式![]() 成立.
成立.
所以![]()
![]()
![]()
即![]() .
.
【試題解析】
【高考考點】本小題主要考查函數的單調性、最值、不等式、數列等基本知識,考查運用導數研究函數性質的方法,考查分析問題和解決問題的能力,滿分14分.
【易錯提醒】第一問中導數記不住公式


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數學 來源: 題型:
(福建卷理22)已知函數f(x)=ln(1+x)-x1
(Ⅰ)求f(x)的單調區間;
(Ⅱ)記f(x)在區間![]() (n∈N*)上的最小值為bx令an=ln(1+n)-bx.
(n∈N*)上的最小值為bx令an=ln(1+n)-bx.
(Ⅲ)如果對一切n,不等式![]() 恒成立,求實數c的取值范圍;
恒成立,求實數c的取值范圍;
(Ⅳ)求證: ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com