
 滿足:①對任意
滿足:①對任意 ,
, ;②存在常數(shù)
;②存在常數(shù) ,對任意
,對任意 ,
, ,則稱數(shù)列
,則稱數(shù)列 為“
為“ 數(shù)列”.
數(shù)列”. 的通項為
的通項為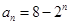
 ,證明:數(shù)列
,證明:數(shù)列 為“
為“ 數(shù)列”;
數(shù)列”; 的各項均為正整數(shù),且數(shù)列
的各項均為正整數(shù),且數(shù)列 為“
為“ 數(shù)列”,證明:對任意
數(shù)列”,證明:對任意 ,
, ;
; 的各項均為正整數(shù),且數(shù)列
的各項均為正整數(shù),且數(shù)列 為“
為“ 數(shù)列”,證明:存在
數(shù)列”,證明:存在 ,數(shù)列
,數(shù)列 為等差數(shù)列.
為等差數(shù)列. ,用單調(diào)性證
,用單調(diào)性證 。(Ⅱ)用反證法證明。即假設存在正整數(shù)
。(Ⅱ)用反證法證明。即假設存在正整數(shù)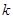 ,使得
,使得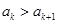 。根據(jù)
。根據(jù)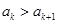 和
和 結(jié)合放縮法推倒論證得出與已知各項均為正整數(shù)相矛盾,則說明假設不成立即原命題成立。(Ⅲ)由(Ⅱ)知
結(jié)合放縮法推倒論證得出與已知各項均為正整數(shù)相矛盾,則說明假設不成立即原命題成立。(Ⅲ)由(Ⅱ)知 ,需分
,需分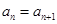 和
和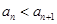 兩種情況討論,結(jié)合已知
兩種情況討論,結(jié)合已知 推理論證,根據(jù)等差的定義可證得存在
推理論證,根據(jù)等差的定義可證得存在  ,數(shù)列
,數(shù)列 為等差數(shù)列.本題的關鍵是當
為等差數(shù)列.本題的關鍵是當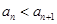 可變形得
可變形得 ,再用累加法表示
,再用累加法表示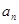 ,即
,即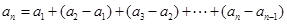 ,根據(jù)
,根據(jù) 進行推理論證。
進行推理論證。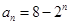 ,可得
,可得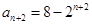 ,
,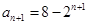 ,
,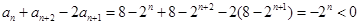 ,
, ,
, .
. 為遞減數(shù)列,所以對任意
為遞減數(shù)列,所以對任意 ,
,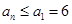 .
. 為“
為“ 數(shù)列”. 5分
數(shù)列”. 5分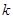 ,使得
,使得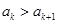 .
. 的各項均為正整數(shù),可得
的各項均為正整數(shù),可得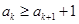 .
.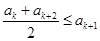 ,可得
,可得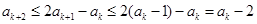 .
.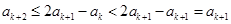 .
.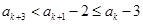 ,
, ,有
,有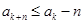 .
.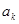 為正整數(shù),設
為正整數(shù),設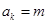 ,則
,則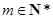 .
.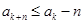 中,設
中,設 ,則
,則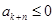 .
. 的各項均為正整數(shù)矛盾.
的各項均為正整數(shù)矛盾. ,
, . 10分
. 10分 為“
為“ 數(shù)列”,
數(shù)列”, ,對任意
,對任意 ,
, .
.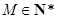 .
. ,
, ,
, .
.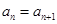 ,則
,則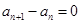 ;若
;若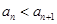 ,則
,則 .
.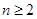 時,有
時,有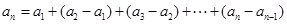 .
.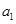 ,
,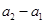 ,
,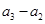 ,
,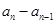 ,中最多有
,中最多有 個大于或等于
個大于或等于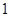 ,
, 矛盾.
矛盾. ,對任意的
,對任意的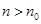 ,有
,有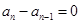 .
. ,
, .
. ,數(shù)列
,數(shù)列 為等差數(shù)列. 14分
為等差數(shù)列. 14分

 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
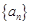 、
、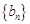 的每一項都是正數(shù),
的每一項都是正數(shù),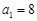 ,
,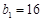 ,且
,且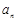 、
、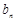 、
、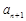 成等差數(shù)列,
成等差數(shù)列,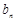 、
、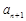 、
、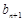 成等比數(shù)列,
成等比數(shù)列,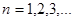 .
.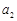 、
、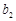 的值;
的值;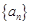 、
、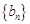 的通項公式;
的通項公式;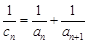 ,證明:對一切正整數(shù)
,證明:對一切正整數(shù)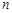 ,有
,有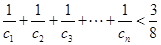 .
.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
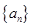 的前
的前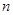 項和為
項和為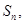 記
記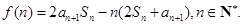
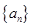 是首項與公差均為
是首項與公差均為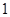 的等差數(shù)列,求
的等差數(shù)列,求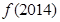 ;
; 且數(shù)列
且數(shù)列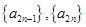 均是公比為
均是公比為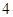 的等比數(shù)列,
的等比數(shù)列,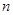 ,
,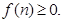
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
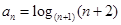
 .我們把使乘積
.我們把使乘積 為整數(shù)的數(shù)n叫做“優(yōu)數(shù)”,則在區(qū)間(1,2004)內(nèi)的所有優(yōu)數(shù)的和為( )
為整數(shù)的數(shù)n叫做“優(yōu)數(shù)”,則在區(qū)間(1,2004)內(nèi)的所有優(yōu)數(shù)的和為( )| A.1024 | B.2003 | C.2026 | D.2048 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com