
(本小題共12分)
已知函數f(x)=2x- -aln(x+1),a∈R.(1)若a=-4,求函數f(x)的單調區間;
-aln(x+1),a∈R.(1)若a=-4,求函數f(x)的單調區間;
(2)求y=f(x)的極值點(即函數取到極值時點的橫坐標).
(1)f(x)的單調增區間為(-1,3), 單調減區間為(3,+∞)。
(2)
ⅰ.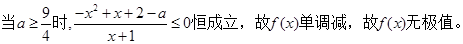 7分
7分
ⅱ.當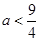 時,
時, 若
若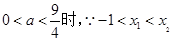 ,由函數的單調性可知f(x)有極小值點
,由函數的單調性可知f(x)有極小值點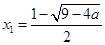 ;有極大值點
;有極大值點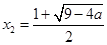 。若
。若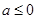 時, f(x)有極大值點
時, f(x)有極大值點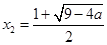 ,無極小值點。
,無極小值點。
【解析】本試題主要是考查了導數在研究函數中的運用。
(1)利用導數的符號與函數單調性的關系求解單調區間。
(2)利用對ad的討論得到函數的單調性,進而得到最值,求解。
請考生在第22、23三題中任選一題做答,如果多做,則按所做的第一題記分.
(1)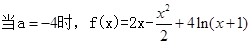
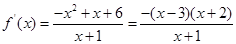
 ……..3分
……..3分
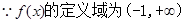 故f(x)的單調增區間為(-1,3), 單調減區間為(3,+∞)………….5分
故f(x)的單調增區間為(-1,3), 單調減區間為(3,+∞)………….5分
(2)∵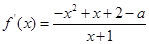
ⅰ.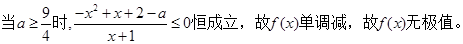 7分
7分
ⅱ.當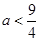 時,對于方程
時,對于方程
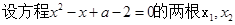 ………………9分
………………9分
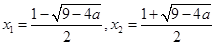
 若
若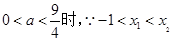 ,由函數的單調性可知f(x)有極小值點
,由函數的單調性可知f(x)有極小值點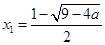 ;有極大值點
;有極大值點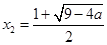 。……………..11分
。……………..11分
若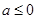 時,
時,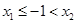 ,由函數的單調性可知f(x)有極大值點
,由函數的單調性可知f(x)有極大值點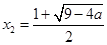 ,無極小值點。………………..12分
,無極小值點。………………..12分


 全能測控一本好卷系列答案
全能測控一本好卷系列答案科目:高中數學 來源: 題型:
. (本小題共12分)已知橢圓E:![]() 的焦點坐
的焦點坐![]() 標為
標為![]() (
(![]() ),點M(
),點M(![]() ,
,![]() )在橢圓E上
)在橢圓E上![]() (1)求橢圓E的方程;(2)O為坐標原點,⊙
(1)求橢圓E的方程;(2)O為坐標原點,⊙![]() 的任意一條切線與橢圓E有兩個交點
的任意一條切線與橢圓E有兩個交點![]() ,
,![]() 且
且![]() ,求⊙
,求⊙![]() 的半徑。
的半徑。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年內蒙古呼倫貝爾市高三第三次模擬考試文科數學試卷 題型:解答題
(本小題共12分)如圖,已知 ⊥平面
⊥平面 ,
, ∥
∥ ,
, 是正三角形,
是正三角形, ,且
,且 是
是 的中點
的中點

(1)求證: ∥平面
∥平面 ;
;
(2)求證:平面BCE⊥平面 .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年內蒙古呼倫貝爾市高三第三次模擬考試文科數學試卷 題型:解答題
(本小題共12分)某中學的高二(1)班男同學有 名,女同學有
名,女同學有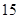 名,老師按照分層抽樣的方法組建了一個
名,老師按照分層抽樣的方法組建了一個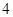 人的課外興趣小組.
人的課外興趣小組.
(Ⅰ)求某同學被抽到的概率及課外興趣小組中男、女同學的人數;
(Ⅱ)經過一個月的學習、討論,這個興趣小組決定選出兩名同學做某項實驗,方法是先從小組里選出 名同學做實驗,該同學做完后,再從小組內剩下的同學中選一名同學做實驗,求選出的兩名同學中恰有一名女同學的概率;
名同學做實驗,該同學做完后,再從小組內剩下的同學中選一名同學做實驗,求選出的兩名同學中恰有一名女同學的概率;
查看答案和解析>>
科目:高中數學 來源:2010-2011學年甘肅省天水市高三上學期第一階段性考試理科數學卷 題型:解答題
(本小題共12分)
如圖,在正三棱柱ABC—A1B1C1中,點D是棱AB的中點,BC=1,AA1=
(1)求證:BC1//平面A1DC;
(2)求二面角D—A1C—A的大小

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com