Question

設不等式組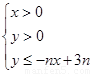所表示的平面區域為D_n，記D_n內 的整點個數為a_n(n∈N^*)(整點即橫坐標和縱坐標均為整數的點)．

(1) 求證：數列{a_n}的通項公式是a_n＝3n(n∈N^*)．

(2) 記數列{a_n}的前n項和為S_n，且T_n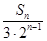＝．若對于一切的正整數n，總有T_n≤m，求實數m的取值范圍．

 

Answer 1

【答案】

(1)詳見試題解析；(2)．

【解析】

試題分析：(1)首先由已知，得，，或，內的整點在直線和上．記直線為，與直線和的交點的縱坐標分別為，則可求得的值，最后可得的表達式；(2)由(1)先求出及的表達式，由已知對一切的正整數，恒成立，等價于，可以利用數列相鄰兩項的差，解，得到數列的最大項，從而可得實數的取值范圍．

試題解析：(1)證明：由，得，，或，內的整點在直線和上．記直線為，與直線和的交點的縱坐標分別為，則，．

(2)，，，∴當時，，且，于是，是數列中的最大項，故．

考點：1．線性規劃整點問題；2．數列通項公式及前項和的求法；3．恒成立不等式中的參數取值范圍問題．