Question

（2009安徽卷理）（本小題滿分13分）

如圖，四棱錐F－ABCD的底面ABCD是菱形，其對角線AC=2，BD=，AE、CF都與平面ABCD垂直，AE=1，CF=2.

（I）求二面角B－AF－D的大小；

（II）求四棱錐E－ABCD與四棱錐F－ABCD公共部分的體積.

Answer 1

解析：本小題主要考查直線與直線、直線與平面、平面與平面的位置關(guān)系、相交平面所成二面角以及空間幾何體的體積計算等知識，考查空間想象能力和推理論證能力、利用綜合法或向量法解決立體幾何問題的能力。本小題滿分13分。

解：（I）（綜合法）連接AC、BD交于菱形的中心O，過O作OGAF，

G為垂足。連接BG、DG。由BDAC，BDCF得BD平面ACF，故BDAF。

于是AF平面BGD，所以BGAF，DGAF，BGD為二面角B－AF－D 的平面角。

由， ，得，          

由，得

（向量法）以A為坐標原點，、、方向分別為x軸、y軸、z軸的正方向建立空間直角坐標系（如圖）

設(shè)平面ABF的法向量，則由得

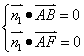令，得，

同理，可求得平面ADF的法向量。         

由知，平面ABF與平面ADF垂直，

二面角B-AF-D的大小等于。

（II）連EB、EC、ED，設(shè)直線AF與直線CE相交于點H，則四棱錐E-ABCD與四棱錐F-ABCD的公共部分為四棱錐H-ABCD。

過H作HP⊥平面ABCD，P為垂足。

因為EA⊥平面ABCD，F(xiàn)C⊥平面ABCD，，所以平面ACFE⊥平面ABCD，從而

由得。

又因為          

故四棱錐H-ABCD的體積