
已知圓錐曲線![]() 的焦點為
的焦點為![]() ,相應的準線方程為
,相應的準線方程為![]() ,且曲線
,且曲線![]() 過定點
過定點![]() .
.
又直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)求曲線![]() 的軌跡方程;
的軌跡方程;
(2)試判斷是否存在直線![]() ,使得點
,使得點![]() 是△
是△![]() 的重心.若存在,求出對應的直線
的重心.若存在,求出對應的直線![]() 的方程;
的方程;
若不存在,請說明理由;
(3)試判斷是否存在直線![]() ,使得點
,使得點![]() 是△
是△![]() 的的垂心.若存在,求出對應的直線
的的垂心.若存在,求出對應的直線![]() 的方程;
的方程;
若不存在,請說明理由.
解:(1)根據圓錐曲線的第二定義知,曲線C的離心率根據圓錐曲線的第二定義知,
曲線C的離心率e=![]() <1,故為橢圓,
<1,故為橢圓,
根據條件解得曲線C的軌跡方程為:![]() . -----------------4分;
. -----------------4分;
(2)假設存在直線l,使得點F是△BMN的重心.
再設直線l與橢圓![]() .的交點M、N的坐標分別為M(x1,y1)、N(x2,y2),
.的交點M、N的坐標分別為M(x1,y1)、N(x2,y2),
則由橢圓幾何性質的范圍性知:-![]() ≤x1≤
≤x1≤![]() , -
, -![]() ≤x2≤
≤x2≤![]() ,則-2
,則-2![]() ≤x1+x2≤2
≤x1+x2≤2![]() <3,
<3,
另一方面,F(1,0)是△BMN的重心, 結合 B(0,1)及重心坐標公式知3×1=0+x1+x2,
即x1+x2=3,這與x1+x2≤2![]() <3矛盾, 故滿足要求的直線l不存在. --------------8分;
<3矛盾, 故滿足要求的直線l不存在. --------------8分;
(3)假設存在直線l,使得點F是△BMN的垂心. 由B(0,1)、F(1,0),知直線BF的斜率為-1. 于是,由BF⊥MN,知直線l的斜率為1. 設直線l方程為y=x+b. 與![]() 聯立消去y,得3x2+4bx+2(b2-1)=0 (*)
聯立消去y,得3x2+4bx+2(b2-1)=0 (*)
設M(x1,y1)、N(x2,y2),根據韋達定理得x1+x2=-![]() , x1x2=
, x1x2=![]() .
.
若再能保證NF⊥BM,即·=0,則F必為△BMN的垂心.
∵=(1-x2,-y2), =(x1,y1-1)
·=(1-x2)x1-y2(y1-1)=x1+y2-x1x2-y1y2=x1+(x2+b)-x1x2-(x1+b)(x2+b)
=-2x1x2+(1-b)(x1+x2)+b-b2=-2·![]() +b-b2=0
+b-b2=0
即3b2+b-4=0,解得b=1或b=-![]() .
.
當b=1時,點B即為直線l與橢圓的交點,不合題意;
當b=-![]() 時,代入方程(*)得3x2-
時,代入方程(*)得3x2-![]() x+
x+![]() =0,其判別式△=
=0,其判別式△=![]() =
=![]() >0,則兩端點存在,
>0,則兩端點存在,
滿足題設.綜上得,存在直線l: y=x-![]() ,使得點F是△BMN的垂心. ---------------------16分
,使得點F是△BMN的垂心. ---------------------16分


科目:高中數學 來源:學習周報 數學 人教課標高二版(A選修1-1) 2009-2010學年 第19期 總第175期 人教課標版(A選修1-1) 題型:044
已知圓錐曲線的焦點為F(-1,1),相應的準線方程為x+y-2=0,且曲線通過坐標原點,求此圓錐曲線方程.
查看答案和解析>>
科目:高中數學 來源:學習周報 數學 人教課標版高二(A選修2-1) 2009-2010學年 第19期 總第175期 人教課標版(A選修2-1) 題型:044
已知圓錐曲線的焦點為F(-1,1),相應的準線方程為x+y-2=0,且曲線通過坐標原點,求此圓錐曲線方程.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖南長沙重點中學高三上學期第四次月考文科數學試卷(解析版) 題型:解答題
已知圓錐曲線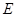 的兩個焦點坐標是
的兩個焦點坐標是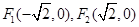 ,且離心率為
,且離心率為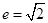 ;
;
(Ⅰ)求曲線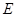 的方程;
的方程;
(Ⅱ)設曲線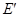 表示曲線
表示曲線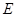 的
的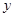 軸左邊部分,若直線
軸左邊部分,若直線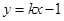 與曲線
與曲線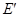 相交于
相交于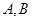 兩點,求
兩點,求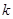 的取值范圍;
的取值范圍;
(Ⅲ)在條件(Ⅱ)下,如果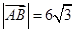 ,且曲線
,且曲線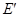 上存在點
上存在點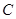 ,使
,使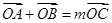 ,求
,求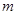 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2013屆遼寧省高三第四次階段測試文科數學試卷(解析版) 題型:解答題
已知圓錐曲線C:
 為參數)和定點
為參數)和定點 ,
, 是此圓錐曲線的左、右焦點。
是此圓錐曲線的左、右焦點。
(1)以原點O為極點,以x軸的正半軸為極軸建立極坐標系,求直線 的極坐標方程;
的極坐標方程;
(2)經過點 ,且與直線
,且與直線 垂直的直線
垂直的直線 交此圓錐曲線于
交此圓錐曲線于 兩點,求
兩點,求 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com