
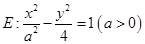 的中心為原點
的中心為原點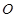 ,左、右焦點分別為
,左、右焦點分別為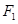 、
、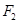 ,離心率為
,離心率為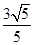 ,點
,點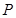 是直線
是直線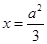 上任意一點,點
上任意一點,點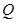 在雙曲線
在雙曲線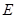 上,且滿足
上,且滿足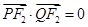 .
.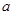 的值;
的值;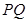 與直線
與直線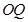 的斜率之積是定值;
的斜率之積是定值;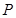 的縱坐標為
的縱坐標為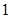 ,過點
,過點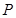 作動直線
作動直線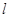 與雙曲線右支交于不同的兩點
與雙曲線右支交于不同的兩點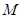 、
、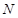 ,在線段
,在線段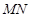 上去異于點
上去異于點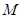 、
、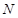 的點
的點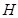 ,滿足
,滿足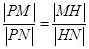 ,證明點
,證明點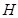 恒在一條定直線上.
恒在一條定直線上.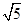 ;(2)詳見解析;(3)詳見解析.
;(2)詳見解析;(3)詳見解析.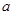 的值;(2)設點
的值;(2)設點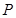 的坐標為
的坐標為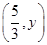 ,點
,點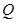 的坐標為
的坐標為 ,利用條件
,利用條件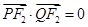 確定
確定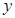 與
與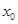 、
、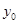 之間的關系,再結合點
之間的關系,再結合點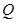 在雙曲線
在雙曲線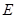 上這一條件,以及斜率公式來證明直線
上這一條件,以及斜率公式來證明直線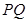 與直線
與直線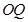 的斜率之積是定值;(3)證法一是先設點
的斜率之積是定值;(3)證法一是先設點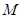 、
、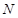 的坐標分別為
的坐標分別為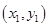 、
、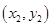 ,結合(2)得到
,結合(2)得到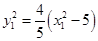 ,
,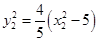 ,引入參數
,引入參數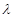 ,利用
,利用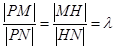 轉化為相應的條件
轉化為相應的條件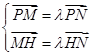 ,利用坐標運算得到點
,利用坐標運算得到點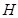 的坐標所滿足的關系式
的坐標所滿足的關系式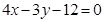 ,進而證明點
,進而證明點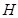 恒在定直線
恒在定直線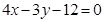 上;證法二是設直線
上;證法二是設直線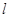 的方程為
的方程為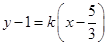 ,將直線
,將直線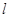 的方程與雙曲線的方程聯立,結合韋達定理,將條件
的方程與雙曲線的方程聯立,結合韋達定理,將條件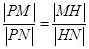 進行等價轉化為
進行等價轉化為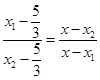 ,結合韋達定理化簡為
,結合韋達定理化簡為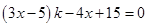 ,最后利用點
,最后利用點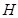 在直線
在直線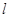 上得到
上得到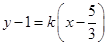 ,從而消去
,從而消去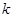 得到
得到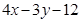
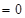 ,進而證明點
,進而證明點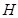 恒在定直線
恒在定直線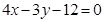 上.
上.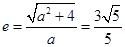 ,由于
,由于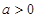 ,解得
,解得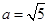 ,
,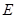 的方程為
的方程為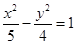 ;
;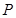 的坐標為
的坐標為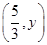 ,點
,點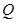 的坐標為
的坐標為 ,易知點
,易知點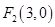 ,
,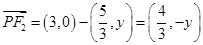 ,
,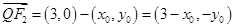 ,
,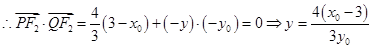 ,因此點
,因此點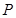 的坐標為
的坐標為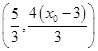 ,
,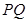 的斜率
的斜率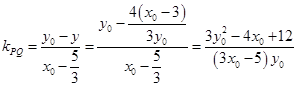 ,直線
,直線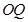 的斜率為
的斜率為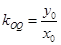 ,
,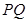 與直線
與直線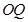 的斜率之積為
的斜率之積為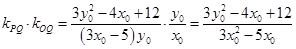 ,
,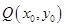 在雙曲線
在雙曲線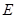 上,所以
上,所以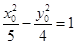 ,所以
,所以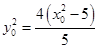 ,
,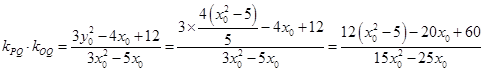
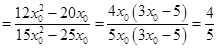 (定值);
(定值);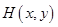 且過點
且過點 的直線
的直線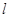 與雙曲線
與雙曲線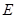 的右支交于不同的兩點
的右支交于不同的兩點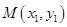 、
、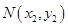 ,由(2)知,
,由(2)知,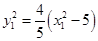 ,
,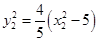 ,
,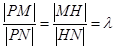 ,則
,則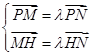 ,即
,即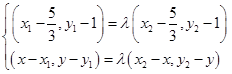 ,
, ,
,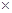 ③,②
③,②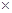 ④得,
④得,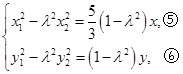 ,
,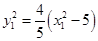 ,
,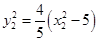 ,代入⑥得
,代入⑥得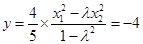 ,⑦,
,⑦,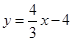 ,即點
,即點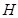 恒在定直線
恒在定直線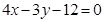 上;
上;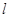 的斜率
的斜率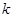 存在,設直線
存在,設直線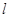 的方程為
的方程為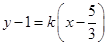 ,
,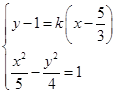 ,
,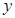 得
得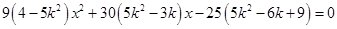 ,
,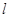 與雙曲線
與雙曲線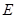 的右支交于不同的兩點
的右支交于不同的兩點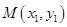 、
、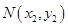 ,
,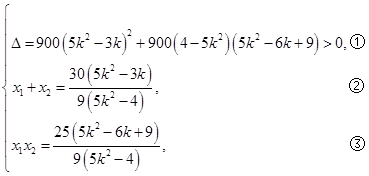 ,
,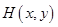 ,由
,由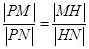 ,得
,得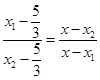 ,
,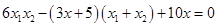 ,
,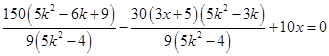 ,
,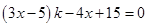 ,④
,④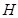 在直線
在直線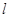 上,所以
上,所以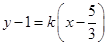 ,⑤
,⑤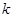 得
得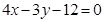 ,所以點
,所以點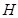 恒在定直線
恒在定直線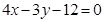 .
.

科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
 π,直線l1經過點A(3,2)和B(a,-1),且直線l1與直線l垂直,直線l2的方程為2x+by+1=0,且直線l2與直線l1平行,則a+b等于 .
π,直線l1經過點A(3,2)和B(a,-1),且直線l1與直線l垂直,直線l2的方程為2x+by+1=0,且直線l2與直線l1平行,則a+b等于 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com