
(本題滿分16分)如圖:AD=2,AB=4的長方形 所在平面與正
所在平面與正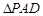 所在平面互相垂直,
所在平面互相垂直,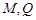 分別為
分別為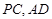 的中點.
的中點.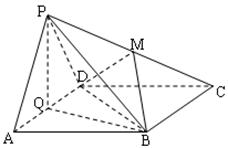
(1)求四棱錐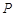 -
- 的體積;
的體積;
(2)求證: 平面
平面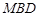 ;
;
(3)試問:在線段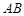 上是否存在一點
上是否存在一點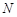 ,使得平面
,使得平面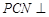 平面
平面 ?若存在,試指出點
?若存在,試指出點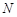 的位置,并證明你的結論;若不存在,請說明理由.
的位置,并證明你的結論;若不存在,請說明理由.
(1)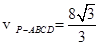 ;(2)連
;(2)連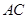 交
交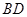 于
于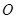 ,連
,連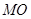 則
則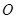 為
為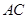 中點,因為
中點,因為 為
為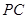 中點,所以
中點,所以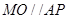 ,又
,又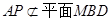 ,
,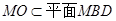 ,則
,則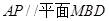 .
.
(3)當BN=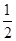 時,平面
時,平面 .
.
解析試題分析:(1)解:正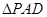 中,Q為
中,Q為 的中點故
的中點故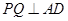
由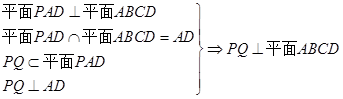 .
. 
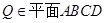
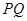 長為
長為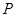 到平面
到平面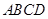 的距離.因為
的距離.因為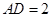 ,所以
,所以
所以, 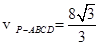
(2)證明:連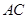 交
交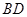 于
于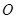 ,連
,連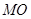 則
則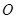 為
為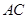 中點,因為
中點,因為 為
為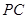 中點,
中點,
所以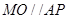 , 又
, 又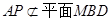 ,
,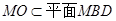 ,則
,則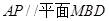 .
.
(3)當BN=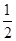 時,平面
時,平面 .
.
證明如下:由(1)證明知 ,又
,又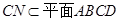 ,則
,則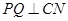
又因為長方形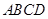 中由相似三角形得,則
中由相似三角形得,則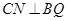
 又
又
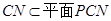 所以,平面
所以,平面 .
.
考點:本題考查了空間中的線面關系
點評:空間問題中的線面關系的證明主要是應用線面平行與垂直的判定定理或性質,具體問題中要是能夠根據題意適當做輔助線;求簡單幾何體的體積問題關鍵是能夠應用轉化思想,將所求幾何體的體積轉化為易于求解底面積和高的幾何體的體積,注意對等積法的應用.


科目:高中數學 來源: 題型:解答題
(本題12分)在直角梯形PBCD中,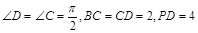 ,A為PD的中點,如下左圖。將
,A為PD的中點,如下左圖。將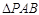 沿AB折到
沿AB折到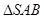 的位置,使
的位置,使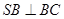 ,點E在SD上,且
,點E在SD上,且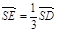 ,如下圖。
,如下圖。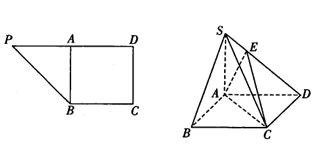
(1)求證: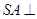 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(14分)如圖,在三棱錐S—ABC中, 是邊長為4的正三角形,平面SAC⊥平面ABC,SA =" SC" =
是邊長為4的正三角形,平面SAC⊥平面ABC,SA =" SC" = ,M、N分別為AB、SB的中點。
,M、N分別為AB、SB的中點。
⑴ 求證:AC⊥SB;
⑵ 求二面角N—CM—B的正切值;
⑶ 求點B到平面CMN的距離。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題12分)如圖,在多面體ABCDEF中,底面ABCD是 平行四邊形,AB=2EF,EF∥AB,,H為BC的中點.求證:FH∥平面EDB.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
如圖,菱形ABCD與矩形BDEF所在平面互相垂直, .
.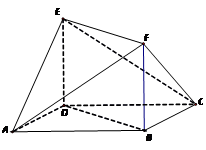
(1)求證:FC∥平面AED;
(2)若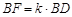 ,當二面角
,當二面角 為直二面角時,求k的值.
為直二面角時,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
如圖所示,四棱錐P-ABCD的底面ABCD是邊長為1的菱形, BCD=60
BCD=60 ,E是CD的中點,PA
,E是CD的中點,PA 底面ABCD,PA=2.
底面ABCD,PA=2.
(1)證明:平面PBE 平面PAB;
平面PAB;
(2)求PC與平面PAB所成角的余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,PA垂直于矩形ABCD所在的平面,AD=PA=2, ,E、F分別是AB、PD的中點.
,E、F分別是AB、PD的中點.
(Ⅰ)求證:平面PCE  平面PCD;
平面PCD;
(Ⅱ)求四面體PEFC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)
如圖,在四面體PABC中,PA=PB,CA=CB,D、E、F、G分別是PA,AC、CB、BP的中點.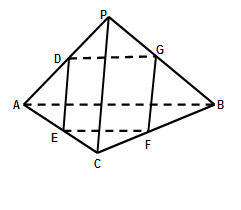
(1)求證:D、E、F、G四點共面;
(2)求證:PC⊥AB;
(3)若△ABC和△PAB都是等腰直角三角形,且AB=2,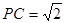 ,求四面體PABC的體積.
,求四面體PABC的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com