
|


科目:高中數學 來源: 題型:
| t2 | 2 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年安徽省合肥32中高三(上)9月月考數學試卷(文科)(解析版) 題型:解答題
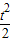 (0≤t≤5),其中t為產品售出的數量(單位:百件).
(0≤t≤5),其中t為產品售出的數量(單位:百件).查看答案和解析>>
科目:高中數學 來源:2011年高考數學復習:2 函數、導數及其應用 質量檢測(1)(解析版) 題型:解答題
 (0≤t≤5),其中t為產品售出的數量(單位:百件).
(0≤t≤5),其中t為產品售出的數量(單位:百件).查看答案和解析>>
科目:高中數學 來源:2011-2012學年安徽省合肥市高三第一次月考文科數學試卷 題型:解答題
(14分)某公司生產一種產品的固定成本為0.5萬元,但每生產100件需再增加成本0.25萬元,市場對此產品的年需求量為500件,年銷售收入(單位:萬元)為R(t)=5t-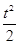 (0≤t≤5),其中t為產品售出的數量(單位:百件).
(0≤t≤5),其中t為產品售出的數量(單位:百件).
(1)把年利潤表示為年產量x(百件)(x≥0)的函數f(x);
(2)當年產量為多少件時,公司可獲得最大年利潤?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com