
 中,角
中,角 、
、 、
、 的對邊分別為
的對邊分別為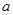 、
、 、
、 ,且滿足
,且滿足

 。
。 的大小;
的大小; ,
, ,試判斷
,試判斷 的形狀,并說明理由
的形狀,并說明理由 (2)等邊三角形
(2)等邊三角形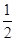 .
. .
.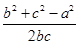 -a·
-a·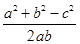 =0,整理得b2+c2-a2=bc,∴cosA=
=0,整理得b2+c2-a2=bc,∴cosA=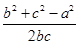 =
=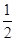 .∵0<A<π,∴A=
.∵0<A<π,∴A= .
.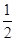 bcsinA=
bcsinA=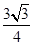 ,即bcsin
,即bcsin =
=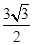 ,
,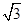 ,∴△ABC為等邊三角形.
,∴△ABC為等邊三角形.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com