
已知函數 的定義域為
的定義域為 . 設點P是函數圖象上的任意一點,過點P分別作直線y=x和y軸的垂線,垂足分別為M、N.
. 設點P是函數圖象上的任意一點,過點P分別作直線y=x和y軸的垂線,垂足分別為M、N.
(1)求證: 是定值;
是定值;
(2)判斷并說明 有最大值還是最小值,并求出此最大值或最小值.
有最大值還是最小值,并求出此最大值或最小值.
 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:解答題
如圖,點 是橢圓
是橢圓 的一個頂點,
的一個頂點, 的長軸是圓
的長軸是圓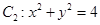 的直徑,
的直徑,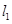 、
、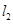 是過點
是過點 且互相垂直的兩條直線,其中
且互相垂直的兩條直線,其中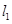 交圓
交圓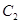 于
于 、
、 兩點,
兩點, 交橢圓
交橢圓 于另一點
于另一點 .
.
(1)求橢圓 的方程;
的方程;
(2)求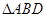 面積的最大值及取得最大值時直線
面積的最大值及取得最大值時直線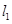 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地需要修建一條大型輸油管道通過240公里寬的沙漠地帶,該段輸油管道兩端的輸油站已建好,余下工程是在該段兩端已建好的輸油站之間鋪設輸油管道和等距離修建增壓站(又稱泵站).經預算,修建一個增壓站的工程費用為400萬元,鋪設距離為x公里的相鄰兩增壓站之間的輸油管道費用為x2+x萬元.設余下工程的總費用為y萬元.
(1)試將y表示成x的函數;
(2)需要修建多少個增壓站才能使y最小,其最小值為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某造紙廠擬建一座平面圖形為矩形且面積為162m2的三級污水處理池,池的深度一定(平面圖如圖所示),如果池四周圍墻建造單價為400元/m2,中間兩道隔墻建造單價為248元/m2,池底建造單價為80元/m2,水池所有墻的厚度忽略不計.
(1)試設計污水處理池的長和寬,使總造價最低,并求出最低總造價;
(2)若由于地形限制,該池的長和寬都不能超過16m,試設計污水池的長和寬,使總造價最低,并求出最低總造價.
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
已知點(3,1)和(- 4,6)在直線3x-2y+a=0的兩側,則a的取值范圍是( )
| A.a<-7或 a>24 | B.a="7" 或 a=24 | C.-7<a<24 | D.-24<a<7 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com