
| π | 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
3
| ||
| 16 |


科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
在“自選模塊”考試中,某試場的每位同學都選了一道數學題,第一小組選《數學史與不等式選講》的有1人,選《矩陣變換和坐標系與參數方程》的有5人,第二小組選《數學史與不等式選講》的有2人,選《矩陣變換和坐標系與參數方程》的有4人,現從第一、第二兩小組各任選2人分析得分情況.
(Ⅰ)求選出的4 人均為選《矩陣變換和坐標系與參數方程》的概率;
(Ⅱ)設![]() 為選出的4個人中選《數學史與不等式選講》的人數,求
為選出的4個人中選《數學史與不等式選講》的人數,求![]() 的分布列和
的分布列和
數學期望.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省三校高三聯考理科數學 題型:解答題
數學自選模塊
題號:03
“數學史與不等式選講”模塊(10分)
已知函數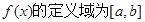 ,且
,且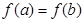 ,對于定義域內的任意實數
,對于定義域內的任意實數
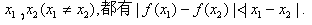 (1)設
(1)設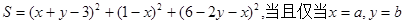 時,S取得最小值,求a,b的值;(2)在(1)的條件下,證明:對任意
時,S取得最小值,求a,b的值;(2)在(1)的條件下,證明:對任意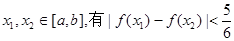 成立.
成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com