考點(diǎn):逆變換與逆矩陣
專題:選作題,矩陣和變換
分析:先求出矩陣A,再求矩陣A的特征值.
解答:解:因?yàn)锳
-1A=E,所以A=(A
-1)
-1.
因?yàn)閨A
-1|=-
,所以A=(A
-1)
-1=
. …(5分)
于是矩陣A的特征多項(xiàng)式為f(λ)=
=λ
2-3λ-4,…(8分)
令f(λ)=0,解得A的特征值λ
1=-1,λ
2=4.…(10分)
點(diǎn)評(píng):本題考查矩陣的逆矩陣,考查特征值.正確求矩陣的逆矩陣是關(guān)鍵.
練習(xí)冊(cè)系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
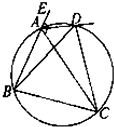
如圖,△ABC的外角平分線AD交外接圓于D,若DB=
,則DC=
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知正數(shù)a,b滿足a+b=2,則行列式
的最小值為
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
若關(guān)于x,y,z的線性方程組增廣矩陣變換為
,方程組的解為
,則m•n=
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知二階矩陣M有特征值λ=1及對(duì)應(yīng)的一個(gè)特征向量
e1=,且M
=
.求矩陣M.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
在平面直角坐標(biāo)系中,曲線C:x
2-y
2=36經(jīng)過伸縮變換
后,所得曲線的焦點(diǎn)坐標(biāo)為( )
| A、(0,±) |
| B、(±,0) |
| C、(0,±) |
| D、(±,0) |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知f(x)為偶函數(shù),當(dāng)x≥0時(shí),f(x)=2a|x-1|-a,若函數(shù)y=f(f(x))恰有10個(gè)零點(diǎn),則a的取值范圍是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
對(duì)于集合
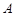
,如果定義了一種運(yùn)算“
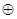
”,使得集合
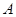
中的元素間滿足下列4個(gè)條件:
(ⅰ)
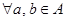
,都有
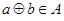
;
(ⅱ)

,使得對(duì)

,都有
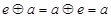
;
(ⅲ)

,

,使得

;
(ⅳ)
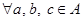
,都有

,
則稱集合
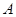
對(duì)于運(yùn)算“
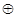
”構(gòu)成“對(duì)稱集”.
下面給出三個(gè)集合及相應(yīng)的運(yùn)算“
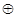
”:
①

,運(yùn)算“
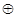
”為普通加法;
②

,運(yùn)算“
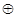
”為普通減法;
③

,運(yùn)算“
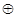
”為普通乘法.
其中可以構(gòu)成“對(duì)稱集”的有
.(把所有正確的序號(hào)都填上)
查看答案和解析>>


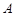 ,如果定義了一種運(yùn)算“
,如果定義了一種運(yùn)算“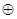 ”,使得集合
”,使得集合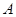 中的元素間滿足下列4個(gè)條件:
中的元素間滿足下列4個(gè)條件: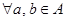 ,都有
,都有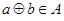 ;
; ,使得對(duì)
,使得對(duì) ,都有
,都有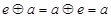 ;
; ,
, ,使得
,使得 ;
;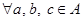 ,都有
,都有 ,
,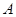 對(duì)于運(yùn)算“
對(duì)于運(yùn)算“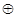 ”構(gòu)成“對(duì)稱集”.
”構(gòu)成“對(duì)稱集”.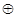 ”:
”: ,運(yùn)算“
,運(yùn)算“ ”為普通加法;
”為普通加法; ,運(yùn)算“
,運(yùn)算“ ”為普通減法;
”為普通減法; ,運(yùn)算“
,運(yùn)算“ ”為普通乘法.
”為普通乘法.