
(本小題滿分14分)
已知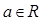 ,函數
,函數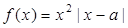 .
.
(Ⅰ)當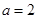 時,求使
時,求使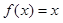 成立的
成立的 的集合;
的集合;
(Ⅱ)求函數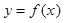 在區間
在區間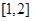 上的最小值.
上的最小值.
(Ⅰ) 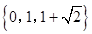 (Ⅱ)最小值為
(Ⅱ)最小值為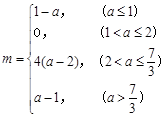
解析試題分析:(Ⅰ)由題意,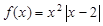 .
.
當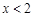 時,
時,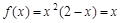 ,解得
,解得 或
或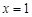 ;
;
當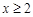 時,
時,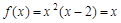 ,解得
,解得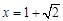 .
.
綜上,所求解集為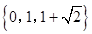 .
.
(Ⅱ)設此最小值為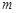 .
.
①當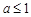 時,在區間
時,在區間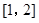 上,
上,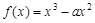 .
.
因為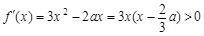 ,
,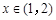 ,
,
則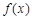 在區間
在區間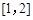 上是增函數,所以
上是增函數,所以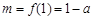 .
.
②當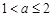 時,在區間
時,在區間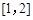 上,
上,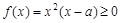 ,由
,由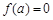 知
知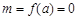 .
.
③當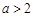 時,在區間
時,在區間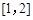 上,
上,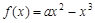 .
.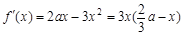 .
.
若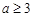 ,在區間
,在區間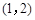 內
內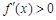 ,從而
,從而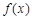 為區間
為區間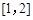 上的增函數,
上的增函數,
由此得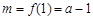 .
.
若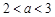 ,則
,則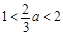 .
.
當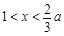 時,
時,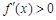 ,從而
,從而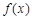 為區間
為區間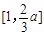 上的增函數;
上的增函數;
當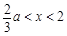 時,
時,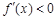 ,從而
,從而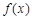 為區間
為區間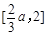 上的減函數.
上的減函數.
因此,當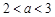 時,
時,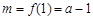 或
或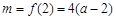 .
.
當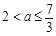 時,
時,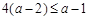 ,故
,故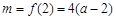 ;
;
當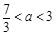 時,
時,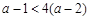 ,故
,故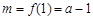 .
.
綜上所述,所求函數的最小值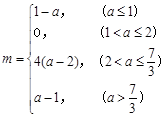
考點:本小題主要考查含絕對值的函數的最值的求法和利用導數求函數的最值,考查學生分類討論思想的應用和運算求解能力.
點評:求解含絕對值的不等式或函數問題,關鍵是通過討論去掉絕對值符號,討論的時候要注意做到“不重不漏”.


 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分16分)
已知二次函數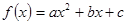 .
.
(1)設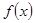 在
在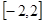 上的最大值、最小值分別是
上的最大值、最小值分別是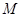 、
、 ,集合
,集合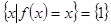 ,且
,且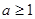 ,記
,記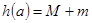 ,求
,求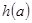 的最小值.
的最小值.
(2)當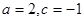 時,
時,
①設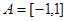 ,不等式
,不等式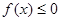 的解集為C,且
的解集為C,且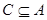 ,求實數
,求實數 的取值范圍;
的取值范圍;
②設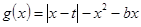
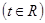 ,求
,求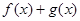 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題共12分)水庫的蓄水量隨時間而變化,現用t表示時間,以月為單位,年初為起點,根據歷年數據,某水庫的蓄水量(單位:億立方米)關于t的近似函數關系式為
V(t)=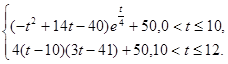
(Ⅰ)該水庫的蓄水量小于50的時期稱為枯水期.以i-1<t<i表示第i月份(i=1,2,…,12),問一年內哪幾個月份是枯水期?
(Ⅱ)求一年內該水庫的最大蓄水量(取e=2.7計算).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某企業為打入國際市場,決定從A、B兩種產品中只選擇一種進行投資生產.已
知投資生產這兩種產品的有關數據如下表:(單位:萬美元)
| 項目類別 | 年固定成本 | 每件產品成本 | 每件產品銷售價 | 每年最多可生產的件數 |
| A產品 | 10 | m | 5 | 100 |
| B產品 | 20 | 4 | 9 | 60 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com