已知平面內(nèi)一動點P到點F(1,0)的距離與點P到y(tǒng)軸的距離的差等于1.
(1)求動點P的軌跡C的方程.
(2)過點F作兩條斜率存在且互相垂直的直線l
1,l
2,設(shè)l
1與軌跡C相交于點A,B,l
2與軌跡C相交于點D,E,求
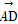
·
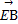
的最小值.
(1) y2=4x(x≥0)和y=0(x<0) (2) 16
(1)設(shè)動點P的坐標(biāo)為(x,y),由題意得

-|x|=1.化簡得y
2=2x+2|x|,
當(dāng)x≥0時,y
2=4x;當(dāng)x<0時,y=0.
所以動點P的軌跡C的方程為
y
2=4x(x≥0)和y=0(x<0).
(2)由題意知,直線l
1的斜率存在且不為0,設(shè)為k,則l
1的方程為y=k(x-1).
由
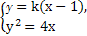
得k
2x
2-(2k
2+4)x+k
2=0.
設(shè)A(x
1,y
1),B(x
2,y
2),則x
1,x
2是上述方程的兩個實根,于是x
1+x
2=2+

,x
1x
2=1.
因為l
1⊥l
2,所以l
2的斜率為-

.
設(shè)D(x
3,y
3),E(x
4, y
4),
則同理可得x
3+x
4=2+4k
2,x
3x
4=1.
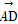
·
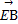
=(

+
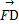
)·(

+
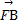
)
=

·

+

·
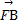
+
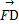
·

+
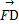
·
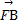
=

·
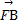
+
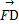
·

=|

|·|
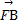
|+|
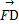
|·|

|
=(x
1+1)(x
2+1)+(x
3+1)(x
4+1)
=x
1x
2+(x
1+x
2)+1+x
3x
4+(x
3+x
4)+1
=1+(2+

)+1+1+(2+4k
2)+1
=8+4(k
2+
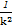
)≥8+4×2

=16.
故當(dāng)且僅當(dāng)k
2=
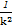
,即k=±1時,
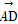
·
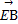
取最小值16.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知平面上三個向量
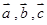
,其中

.
(1)若
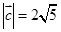
,且
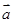
∥
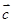
,求
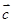
的坐標(biāo);
(2)若
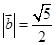
,且
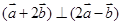
,求
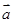
與
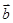
夾角
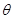
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知直角坐標(biāo)平面中,
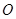
為坐標(biāo)原點,
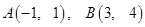
.
(1)求
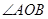
的大小(結(jié)果用反三角函數(shù)值表示);
(2)設(shè)點

為
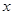
軸上一點,求
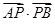
的最大值及取得最大值時點

的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知
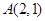
,
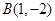
,

,動點

滿足
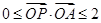
且

,則點
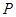
到點

的距離大于

的概率為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知在△ABC中,AB=AC=4,BC=4
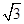
,點P為邊BC所在直線上的一個動點,則關(guān)于

·(
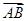
+

)的值,下列選項正確的是( )
| A.最大值為16 | B.為定值8 |
| C.最小值為4 | D.與P的位置有關(guān) |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知兩個單位向量e
1、e
2的夾角為

,若向量b
1=e
1-2e
2,b
2=3e
1+4e
2,則b
1·b
2=________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若向量
a,
b滿足|
a|=|
b|=|
a+
b|=1,則
a·b的值為( )
A.-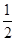 | B.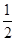 | C.-1 | D.1 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
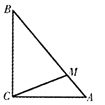
如圖,△ABC中,∠C =90°,且AC=BC=4,點M滿足
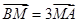
,則
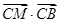
=( )
查看答案和解析>>

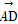 ·
·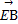 的最小值.
的最小值. -|x|=1.化簡得y2=2x+2|x|,
-|x|=1.化簡得y2=2x+2|x|,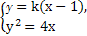 得k2x2-(2k2+4)x+k2=0.
得k2x2-(2k2+4)x+k2=0. ,x1x2=1.
,x1x2=1. .
.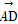 ·
·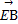 =(
=( +
+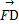 )·(
)·( +
+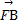 )
) ·
· +
+ ·
·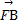 +
+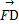 ·
· +
+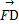 ·
·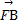
 ·
·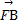 +
+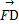 ·
· =|
=| |·|
|·|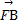 |+|
|+|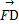 |·|
|·| |
| )+1+1+(2+4k2)+1
)+1+1+(2+4k2)+1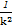 )≥8+4×2
)≥8+4×2 =16.
=16.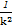 ,即k=±1時,
,即k=±1時,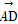 ·
·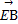 取最小值16.
取最小值16.

 新課標(biāo)階梯閱讀訓(xùn)練系列答案
新課標(biāo)階梯閱讀訓(xùn)練系列答案 口算心算速算應(yīng)用題系列答案
口算心算速算應(yīng)用題系列答案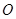 為坐標(biāo)原點,
為坐標(biāo)原點,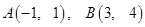 .
.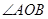 的大小(結(jié)果用反三角函數(shù)值表示);
的大小(結(jié)果用反三角函數(shù)值表示); 為
為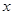 軸上一點,求
軸上一點,求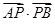 的最大值及取得最大值時點
的最大值及取得最大值時點 的坐標(biāo).
的坐標(biāo).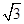 ,點P為邊BC所在直線上的一個動點,則關(guān)于
,點P為邊BC所在直線上的一個動點,則關(guān)于 ·(
·(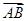 +
+ )的值,下列選項正確的是( )
)的值,下列選項正確的是( )