
 滿足
滿足 ,
, ,
, ,
, 是數列
是數列 的前
的前 項和.
項和. 為等差數列.
為等差數列. ;
; 滿足
滿足 ,數列
,數列 滿足
滿足 ,試比較數列
,試比較數列 前
前 項和
項和 與
與 前
前 項和
項和 的大小;
的大小; ,
, 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.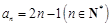
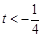 或
或 時,
時,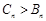 ;當
;當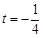 或
或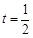 時,
時,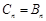 ;當
;當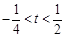 時,
時,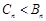
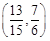
 與
與 關系出發,得出
關系出發,得出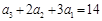 ,利用
,利用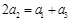 解出
解出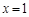 ,從而解出首項與公差,②
,從而解出首項與公差,② 實際是一個等比數列,分別求出數列
實際是一個等比數列,分別求出數列 前
前 項和
項和 與
與 前
前 項和
項和 ,要使計算簡便,需用
,要使計算簡便,需用 表示
表示 ,比較兩者大小通常用作差法. 作差法的關鍵是因式分解,將差分解為因子,根據因子的符號討論差的正負,從而確定大小,(2) 不等式恒成立問題,首先化簡不等式. 需從
,比較兩者大小通常用作差法. 作差法的關鍵是因式分解,將差分解為因子,根據因子的符號討論差的正負,從而確定大小,(2) 不等式恒成立問題,首先化簡不等式. 需從 與
與 關系出發,得出項的關系:
關系出發,得出項的關系: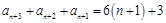 ,這是三項之間的關系,需繼續化簡成兩項之間關系:
,這是三項之間的關系,需繼續化簡成兩項之間關系: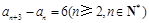 ,這樣原數列分解為三個等差數列,則
,這樣原數列分解為三個等差數列,則 恒成立等價轉化為
恒成立等價轉化為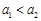 且
且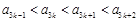 ,代入可解得
,代入可解得
 ,所以
,所以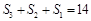 ,
,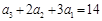 ,又
,又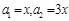 ,所以
,所以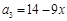 , 2分
, 2分 成等差數列,所以
成等差數列,所以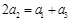 ,即
,即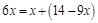 ,解得
,解得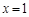 ,
, ; 4分
; 4分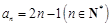 ,所以
,所以 ,其前
,其前 項和
項和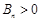 ,
, , 5分
, 5分 項和
項和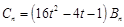 ,所以
,所以 , 7分
, 7分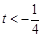 或
或 時,
時,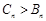 ;當
;當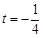 或
或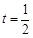 時,
時,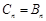 ;
;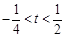 時,
時,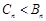 9分
9分 知
知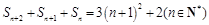 ,
,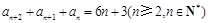 , 10分
, 10分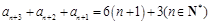 ,作差得
,作差得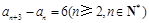 , 11分
, 11分 時,
時,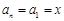 ;
; 時,
時, ;
;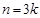 時,
時, ;
;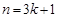 時,
時,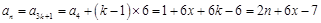 ; 14分
; 14分 ,
, 恒成立,所以
恒成立,所以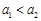 且
且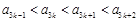 ,
,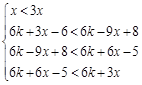 ,解得,
,解得, ,故實數
,故實數 的取值范圍為
的取值范圍為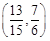 . 16分
. 16分

科目:高中數學 來源:不詳 題型:填空題
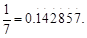 令
令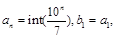 令當n>1時,
令當n>1時,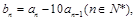 則
則 ,
,  .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com