
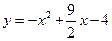 ,通過原點O作C的切線
,通過原點O作C的切線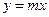 ,使切點P在第一象限.
,使切點P在第一象限. 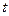 ,為使DOPQ的面積小于DPQR的面積,試求
,為使DOPQ的面積小于DPQR的面積,試求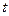 的取值范圍.
的取值范圍. ,P的坐標(biāo)為(2,1)
,P的坐標(biāo)為(2,1) ,-4)
,-4) 范圍為t<
范圍為t<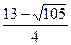 或t>
或t>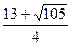 .
.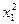 +
+ x1 – 4……②,
x1 – 4……②,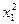 +(k–
+(k– )x1+4=0………
)x1+4=0………
 …………………………………………2分
…………………………………………2分 )2–16=0,得:k=
)2–16=0,得:k= 或k=
或k= ……………………4分
……………………4分 時x1= -2,y1= -1
時x1= -2,y1= -1 7;當(dāng)k=
7;當(dāng)k= 時,x1= 2,y1= 1;
時,x1= 2,y1= 1; ,P的坐標(biāo)為(2,1),……………6分
,P的坐標(biāo)為(2,1),……………6分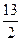 x+9=0,設(shè)Q點的坐標(biāo)為(x2, y2),則2x2=9,所以x2=
x+9=0,設(shè)Q點的坐標(biāo)為(x2, y2),則2x2=9,所以x2= ,y2=-4,
,y2=-4, ,-4),………………………
,-4),……………………… ………
……… ………………10分
………………10分 t–4),它到直線PQ的距離為:
t–4),它到直線PQ的距離為: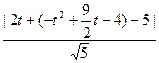 =
=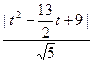 ……………………………………12分
……………………………………12分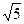 ,SDOPQ=
,SDOPQ= ´PQ´OP,SDPQR=
´PQ´OP,SDPQR= ´PQ´d,
´PQ´d, 即:
即: OP < d,即:
OP < d,即: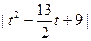 >5,……………………………………14分
>5,……………………………………14分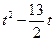 +4>0或
+4>0或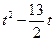 +14<0
+14<0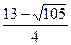 或t>
或t>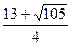
 范圍為t<
范圍為t<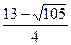 或t>
或t>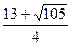 .……………………………16分
.……………………………16分

科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
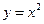 和三個點
和三個點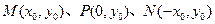
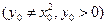 ,過點
,過點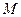 的一條直線交拋物線于
的一條直線交拋物線于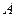 、
、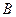 兩點,
兩點,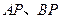 的延長線分別交曲線
的延長線分別交曲線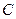 于
于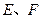 .
.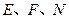 三點共線;
三點共線;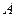 、
、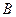 、
、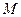 、
、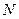 四點共線,問:是否存在
四點共線,問:是否存在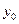 ,使以線段
,使以線段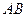 為直徑的圓與拋物線有異于
為直徑的圓與拋物線有異于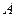 、
、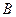 的交點?如果存在,求出
的交點?如果存在,求出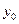 的取值范圍,并求出該交點到直線
的取值范圍,并求出該交點到直線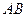 的距離;若不存在,請說明理由.
的距離;若不存在,請說明理由.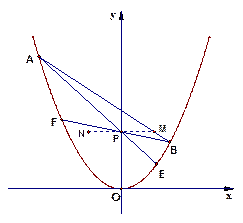
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
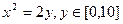 ,在杯內(nèi)放入一個清潔球,要求清潔球能擦凈酒杯的最底部(如圖),則清潔球的最大半徑為
,在杯內(nèi)放入一個清潔球,要求清潔球能擦凈酒杯的最底部(如圖),則清潔球的最大半徑為 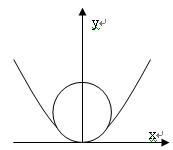
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com