Question

正四棱錐的側棱長為，底面邊長為，為中點，則異面直線與所成的角是      ．

Answer 1

 

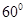
解析試題分析：連接底面正方形ABCD對角線AC、BD，取底面ABCD對角線AC的中點F，連接EF，BD，說明EF與BE的成角是BE與SC的成角，通過在△BFE中根據余弦定理，BF²=EF²+BE²-2EF•BEcos∠BEF，求出cos∠BEF解得異面直線BE與SC所成角的大小．
連接底面正方形ABCD對角線AC、BD，取底面ABCD對角線AC的中點F，連接EF，BD，EF是三角形ASC的中位線，EF∥SC，且EF=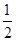SC，則EF與BE的成角是BE與SC的成角， BF=，AB=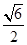
，EF=,三角形SAB是等腰三角形，從S作SG⊥AB，
cosA==,根據余弦定理，BE²=AE²+AB²-2AE•AB•cosA=2，BE=,在△BFE中根據余弦定理，BF²=EF²+BE²-2EF•BEcos∠BEF，cos∠BEF=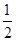，∠BEF=60°；
異面直線BE與SC所成角的大小60°．
故答案為：60°
考點：本題主要是考查異面直線及其所成的角，考查計算能力，是基礎題
點評：解決該試題的關鍵是利用平移法得到相交直線的夾角，即為異面直線所成的角。進而得到結論。