已知等式

對

,恒成立,寫出所有滿足題設的數(shù)對

=_____________________.
試題分析:因為等式

對

,恒成立.所以

.所以

對

,恒成立.只有滿足
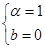
才有可能成立.故填(1,0).本小題的關鍵是恒成立的問題.左右兩邊的對應項的系數(shù)相等.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
設函數(shù)

(I)求函數(shù)

的單調區(qū)間;
(II)若不等式

(

)在

上恒成立,求

的最大值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如果函數(shù)
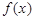
滿足在集合
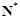
上的值域仍是集合
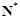
,則把函數(shù)
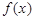
稱為N函數(shù).
例如:
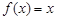
就是N函數(shù).
(Ⅰ)判斷下列函數(shù):①
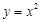
,②
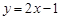
,③
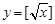
中,哪些是N函數(shù)?(只需寫出判斷結果);
(Ⅱ)判斷函數(shù)
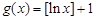
是否為N函數(shù),并證明你的結論;
(Ⅲ)證明:對于任意實數(shù)
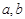
,函數(shù)
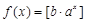
都不是N函數(shù).
(注:“
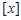
”表示不超過
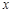
的最大整數(shù))
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
函數(shù)f(x)=lg x-

的零點所在的區(qū)間是( ).
| A.(3,4) | B.(2,3) |
| C.(1,2) | D.(0,1) |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如果二次函數(shù)

不存在零點,則

的取值范圍是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
定義域為R的函數(shù)

滿足

,且當
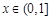
時,

,則當

時,

的最小值為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知函數(shù)

是R上的可導函數(shù),當

時,有

,則函數(shù)

的零點個數(shù)是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若
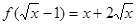
,則f(x)=
| A.x2+4x+3(x∈R) | B.x2+4x(x∈R) |
| C.x2+4x(x≥-1) | D.x2+4x+3(x≥-1) |
查看答案和解析>>

 對
對 ,恒成立,寫出所有滿足題設的數(shù)對
,恒成立,寫出所有滿足題設的數(shù)對 =_____________________.
=_____________________.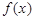 滿足在集合
滿足在集合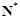 上的值域仍是集合
上的值域仍是集合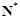 ,則把函數(shù)
,則把函數(shù)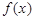 稱為N函數(shù).
稱為N函數(shù).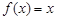 就是N函數(shù).
就是N函數(shù).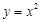 ,②
,②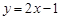 ,③
,③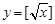 中,哪些是N函數(shù)?(只需寫出判斷結果);
中,哪些是N函數(shù)?(只需寫出判斷結果);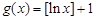 是否為N函數(shù),并證明你的結論;
是否為N函數(shù),并證明你的結論;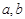 ,函數(shù)
,函數(shù)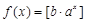 都不是N函數(shù).
都不是N函數(shù).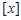 ”表示不超過
”表示不超過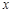 的最大整數(shù))
的最大整數(shù))