Question

(2006全國Ⅰ，19)如下圖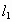，、是互相垂直的異面直線，MN是它們的公垂線段．點A、B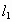在上，C在上，AM=MB=MN．

(1)證明：AC⊥NB；

(2)若∠ACB=60°，求NB與平面ABC所成角的余弦值．

Answer 1

答案：略
解析：

解析：解法一：(1)由已知⊥MN，⊥，MN∩=M，可得⊥平面ABN． 由已知MN⊥，AM=MB=MN，可知AN=NB且AN⊥NB．又AN為AC在平面ABN內的射影．∴AC⊥NB． (2)∵Rt△CNA≌Rt△CNB， ∴AC=BC，又已知∠ACB=60°，因此△ABC為正三角形． ∵Rt△ANB≌Rt△CNB， ∴NC=NA=NB，因此N在平面ABC內的射影H是正三角形ABC的中心，連結BH，∠NBH為NB與平面ABC所成的角． 在Rt△NHB中,． 解法二：如下圖，建立空間直角坐標系M—xyz． 令MN=1，則有A(－1，0，0)，B(1，0，0)，N(0，1，0)． (1)∵MN是、的公垂線，⊥．∴⊥平面ABN． ∴平行于z軸． 故可設C(0，1，m)． 于是=(1，l，m)，(1，－1，0)， ∵=1＋(－1)＋0=0，∴AC⊥NB． (2)∵=(1，1，m)，=(－1，1，m)，∴， 又已知∠ACB=60°，∴△ABC為正三角形，AC=BC=AB=2． 在Rt△CNB中，，可得，故C(0，1，)． 連結MC，作NH⊥MC于H，設H(0，λ，λ)(λ>0)． =(0，1λ，λ)，=(0，1，)． ∵，∴． ∴H，可得， 連結BH，， ∵，∴， 又MC∩BH=H， ∴HN⊥平面ABC，∠NBH為NB與平面ABC所成的角． 又， ∴．

提示：

剖析：用向量法證明線線垂直較好．把幾何問題轉化為代數問題求解．線面角的求法可用綜合法或向量法．