
已知半徑為 的球內有一個內接正方體(即正方體的頂點都在球面上).
的球內有一個內接正方體(即正方體的頂點都在球面上).
(1)求此球的體積;
(2)求此球的內接正方體的體積;
(3)求此球的表面積與其內接正方體的全面積之比.
(1)V=4
 ;(2)V=8;(3)球的表面積與其內接正方體的全面積之比為
;(2)V=8;(3)球的表面積與其內接正方體的全面積之比為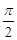 .
.
解析試題分析:(1)球的體積公式為V=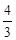
 R3,將R=
R3,將R= 代入可得V=4
代入可得V=4
 ;(2)要求內接正方體的體積,需要知道正方體的棱長,正方體的對角線是球的直徑,而正方體的對角線是棱長的
;(2)要求內接正方體的體積,需要知道正方體的棱長,正方體的對角線是球的直徑,而正方體的對角線是棱長的 倍,設正方體的棱長為a,所以2
倍,設正方體的棱長為a,所以2 =
= a,a="2," V=a3=8;(3)求出正方體的表面積和球的表面積,從而得出球的球面面積與其內接正方體的全面積之比,S球=4
a,a="2," V=a3=8;(3)求出正方體的表面積和球的表面積,從而得出球的球面面積與其內接正方體的全面積之比,S球=4 R2=12
R2=12 ,S正方體=6a2=24,所以這個球的表面積與其內接正方體的全面積之比為12
,S正方體=6a2=24,所以這個球的表面積與其內接正方體的全面積之比為12 :24=
:24=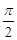 .
.
試題解析:(1)球的體積V=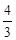
 R3=4
R3=4
 ;
;
(2)設正方體的棱長為a,
∴2 =
=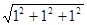 a =
a = a,a="2," V=a3=8;
a,a="2," V=a3=8;
(3)S球=4 R2=12
R2=12 ,
,
S正方體=6a2=24,
∴這個球的表面積與其內接正方體的全面積之比為12 :24=
:24=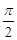 .
.
考點:1.球的體積公式;2.球內接多面體.


科目:高中數學 來源: 題型:解答題
某工廠為了制造一個實心工件,先畫出了這個工件的三視圖(如圖),其中正視圖與側視圖為兩個全等的等腰三角形,俯視圖為一個圓,三視圖尺寸如圖所示(單位cm);
(1)求出這個工件的體積;
(2)工件做好后,要給表面噴漆,已知噴漆費用是每平方厘米1元,現要制作10個這樣的工件,請計算噴漆總費用(精確到整數部分).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知四棱錐 的三視圖和直觀圖如下圖所示,其中正視圖、側視圖是直角三角形,俯視圖是有一條對角線的正方形.
的三視圖和直觀圖如下圖所示,其中正視圖、側視圖是直角三角形,俯視圖是有一條對角線的正方形. 是側棱
是側棱 上的動點.
上的動點.

(1)求證: ;
;
(2)若 為
為 的中點,求直線
的中點,求直線 與平面
與平面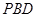 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,三棱柱ABC-A1B1C1的側棱AA1⊥平面ABC,△ABC為正三角形,且側面AA1C1C是邊長為2的正方形,E是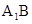 的中點,F在棱CC1上。
的中點,F在棱CC1上。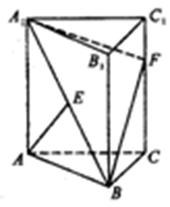
(1)當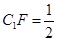 CF時,求多面體ABCFA1的體積;
CF時,求多面體ABCFA1的體積;
(2)當點F使得A1F+BF最小時,判斷直線AE與A1F是否垂直,并證明的結論。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四棱柱ABCD-A1B1C1D1中,已知平面AA1C1C丄平面ABCD,且AB=BC=CA=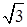 ,AD=CD=1.
,AD=CD=1.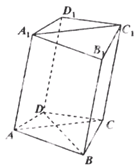
 求證:BD⊥AA1;
求證:BD⊥AA1; 若四邊形
若四邊形 是菱形,且
是菱形,且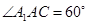 ,求四棱柱
,求四棱柱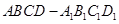 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com