
已知二次函數(shù)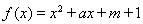 ,關(guān)于x的不等式
,關(guān)于x的不等式 的解集為
的解集為 ,其中m為非零常數(shù).設(shè)
,其中m為非零常數(shù).設(shè)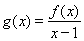 .
.
(1)求a的值;
(2)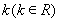 如何取值時(shí),函數(shù)
如何取值時(shí),函數(shù)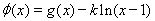 存在極值點(diǎn),并求出極值點(diǎn);
存在極值點(diǎn),并求出極值點(diǎn);
(3)若m=1,且x>0,求證: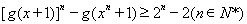
(1)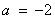 (2)當(dāng)
(2)當(dāng)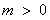 時(shí),
時(shí),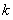 取任何實(shí)數(shù), 函數(shù)
取任何實(shí)數(shù), 函數(shù) 有極小值點(diǎn)
有極小值點(diǎn) ;
;
當(dāng)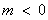 時(shí),
時(shí),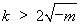 ,函數(shù)
,函數(shù) 有極小值點(diǎn)
有極小值點(diǎn) ,有極大值點(diǎn)
,有極大值點(diǎn)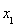 .…9分
.…9分
(其中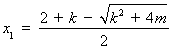 ,
, 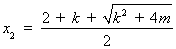 )(3)見(jiàn)解析
)(3)見(jiàn)解析
【解析】(1)【解析】
∵關(guān)于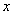 的不等式
的不等式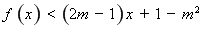 的解集為
的解集為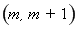 ,
,
即不等式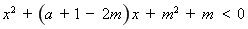 的解集為
的解集為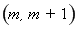 ,
,
∴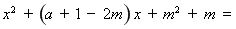
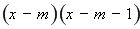 .
.
∴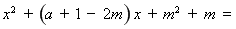
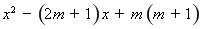 .
.
∴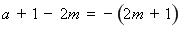 .
.
∴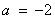 .
.
(2)解法1:由(1)得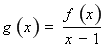
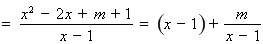 .
.
∴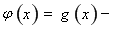
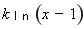
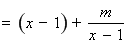
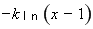 的定義域?yàn)?/span>
的定義域?yàn)?/span>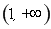 .
.
∴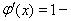
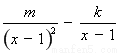
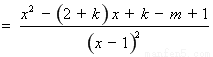 . ………3分
. ………3分
方程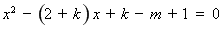 (*)的判別式
(*)的判別式
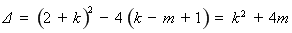 .………4分
.………4分
①當(dāng)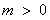 時(shí),
時(shí),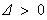 ,方程(*)的兩個(gè)實(shí)根為
,方程(*)的兩個(gè)實(shí)根為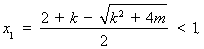
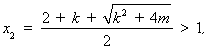 ………5分
………5分
則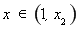 時(shí),
時(shí),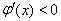 ;
;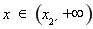 時(shí),
時(shí),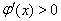 .
.
∴函數(shù) 在
在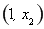 上單調(diào)遞減,在
上單調(diào)遞減,在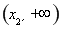 上單調(diào)遞增.
上單調(diào)遞增.
∴函數(shù) 有極小值點(diǎn)
有極小值點(diǎn) . ………6分
. ………6分
②當(dāng)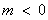 時(shí),由
時(shí),由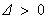 ,得
,得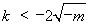 或
或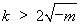 ,
,
若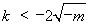 ,則
,則
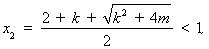
故
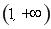 時(shí),
時(shí),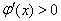 ,
,
∴函數(shù) 在
在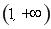 上單調(diào)遞增.
上單調(diào)遞增.
∴函數(shù) 沒(méi)有極值點(diǎn).………7分
沒(méi)有極值點(diǎn).………7分
若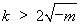 時(shí),
時(shí),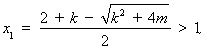
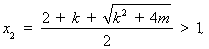
則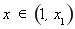 時(shí),
時(shí),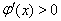 ;
;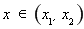 時(shí),
時(shí),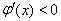 ;
;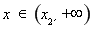 時(shí),
時(shí),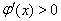 .
.
∴函數(shù) 在
在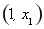 上單調(diào)遞增,在
上單調(diào)遞增,在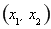 上單調(diào)遞減,在
上單調(diào)遞減,在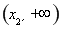 上單調(diào)遞增.
上單調(diào)遞增.
∴函數(shù) 有極小值點(diǎn)
有極小值點(diǎn) ,有極大值點(diǎn)
,有極大值點(diǎn)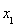 . ………8分
. ………8分
綜上所述, 當(dāng)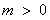 時(shí),
時(shí),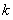 取任意實(shí)數(shù), 函數(shù)
取任意實(shí)數(shù), 函數(shù) 有極小值點(diǎn)
有極小值點(diǎn) ;
;
當(dāng)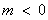 時(shí),
時(shí),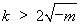 ,函數(shù)
,函數(shù) 有極小值點(diǎn)
有極小值點(diǎn) ,有極大值點(diǎn)
,有極大值點(diǎn)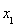 .…9分
.…9分
(其中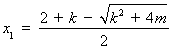 ,
, 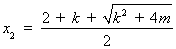 )
)
解法2:由(1)得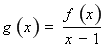
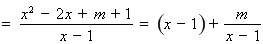 .
.
∴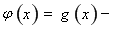
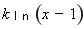
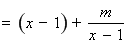
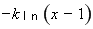 的定義域?yàn)?/span>
的定義域?yàn)?/span>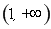 .
.
∴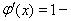
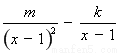
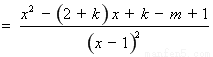 . ………3分
. ………3分
若函數(shù)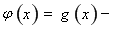
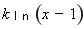 存在極值點(diǎn)等價(jià)于函數(shù)
存在極值點(diǎn)等價(jià)于函數(shù)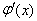 有兩個(gè)不等的零點(diǎn),且
有兩個(gè)不等的零點(diǎn),且
至少有一個(gè)零點(diǎn)在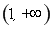 上. ………4分
上. ………4分
令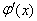
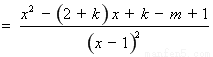
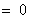 ,
,
得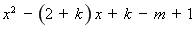
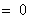 , (*)
, (*)
則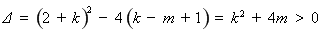 ,(**)…………5分
,(**)…………5分
方程(*)的兩個(gè)實(shí)根為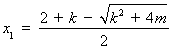 ,
, 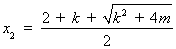 .
.
設(shè)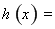
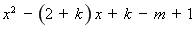 ,
,
①若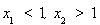 ,則
,則 ,得
,得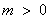 ,此時(shí),
,此時(shí),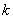 取任意實(shí)數(shù), (**)成立.
取任意實(shí)數(shù), (**)成立.
則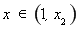 時(shí),
時(shí),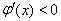 ;
;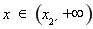 時(shí),
時(shí),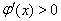 .
.
∴函數(shù) 在
在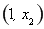 上單調(diào)遞減,在
上單調(diào)遞減,在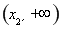 上單調(diào)遞增.
上單調(diào)遞增.
∴函數(shù) 有極小值點(diǎn)
有極小值點(diǎn) . ………6分
. ………6分
②若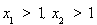 ,則
,則 得
得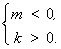
又由(**)解得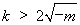 或
或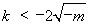 ,
,
故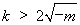 .………7分
.………7分
則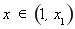 時(shí),
時(shí),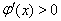 ;
;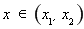 時(shí),
時(shí),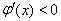 ;
;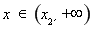 時(shí),
時(shí),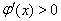 .
.
∴函數(shù) 在
在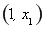 上單調(diào)遞增,在
上單調(diào)遞增,在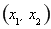 上單調(diào)遞減,在
上單調(diào)遞減,在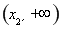 上單調(diào)遞增.
上單調(diào)遞增.
∴函數(shù) 有極小值點(diǎn)
有極小值點(diǎn) ,有極大值點(diǎn)
,有極大值點(diǎn)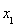 . ………8分
. ………8分
綜上所述, 當(dāng)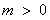 時(shí),
時(shí),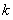 取任何實(shí)數(shù), 函數(shù)
取任何實(shí)數(shù), 函數(shù) 有極小值點(diǎn)
有極小值點(diǎn) ;
;
當(dāng)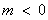 時(shí),
時(shí),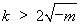 ,函數(shù)
,函數(shù) 有極小值點(diǎn)
有極小值點(diǎn) ,有極大值點(diǎn)
,有極大值點(diǎn)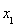 .…9分
.…9分
(其中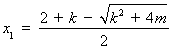 ,
, 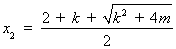 )
)
(3)∵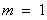 , ∴
, ∴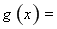
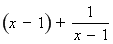 .
.
∴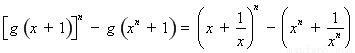
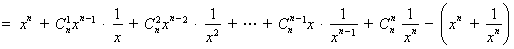
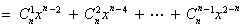 . ………10分
. ………10分
令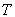
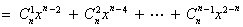 ,
,
則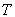

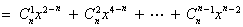 .
.
∵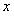
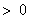 ,
,
∴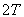
 …11分
…11分
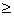
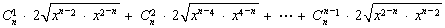 12分
12分
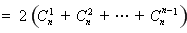

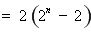 .………13分
.………13分
∴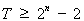 ,即
,即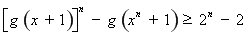 . ……………14分
. ……………14分
證法2:下面用數(shù)學(xué)歸納法證明不等式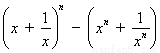
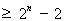 .
.
① 當(dāng)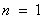 時(shí),左邊
時(shí),左邊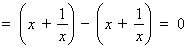 ,右邊
,右邊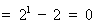 ,不等式成立;
,不等式成立;
………10分
②假設(shè)當(dāng)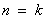
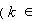 N
N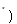 時(shí),不等式成立,即
時(shí),不等式成立,即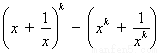
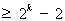 ,
,
則 
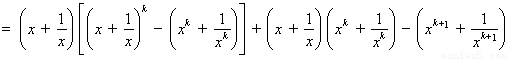
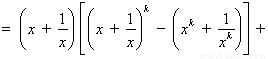
 ………11分
………11分
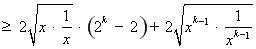 ………12分
………12分
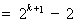 . ………13分
. ………13分
也就是說(shuō),當(dāng)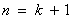 時(shí),不等式也成立.
時(shí),不等式也成立.
由①②可得,對(duì)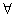
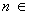 N
N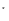 ,
,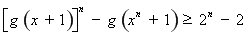 都成立. …14分
都成立. …14分


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:2014年高考數(shù)學(xué)全程總復(fù)習(xí)課時(shí)提升作業(yè)七十二第十章第九節(jié)練習(xí)卷(解析版) 題型:選擇題
利用下列盈利表中的數(shù)據(jù)進(jìn)行決策,應(yīng)選擇的方案是( )
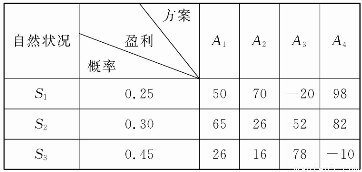
(A)A1 (B)A2 (C)A3 (D)A4
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年高考數(shù)學(xué)全程總復(fù)習(xí)課時(shí)提升作業(yè)七十一第十章第八節(jié)練習(xí)卷(解析版) 題型:填空題
某省實(shí)驗(yàn)中學(xué)高三共有學(xué)生600人,一次數(shù)學(xué)考試的成績(jī)(試卷滿分150分)服從正態(tài)分布N(100,σ2),統(tǒng)計(jì)結(jié)果顯示學(xué)生考試成績(jī)?cè)?/span>80分到100分之間的人數(shù)約占總?cè)藬?shù)的 ,則此次考試成績(jī)不低于120分的學(xué)生約有 人.
,則此次考試成績(jī)不低于120分的學(xué)生約有 人.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年高中數(shù)學(xué)全國(guó)各省市理科導(dǎo)數(shù)精選22道大題練習(xí)卷(解析版) 題型:解答題
設(shè)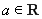 ,函數(shù)
,函數(shù)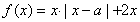 .
.
(1)若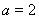 ,求函數(shù)
,求函數(shù)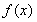 在區(qū)間
在區(qū)間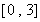 上的最大值;
上的最大值;
(2)若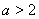 ,寫(xiě)出函數(shù)
,寫(xiě)出函數(shù)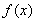 的單調(diào)區(qū)間(不必證明);
的單調(diào)區(qū)間(不必證明);
(3)若存在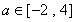 ,使得關(guān)于
,使得關(guān)于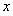 的方程
的方程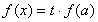 有三個(gè)不相等的實(shí)數(shù)解,求實(shí)數(shù)
有三個(gè)不相等的實(shí)數(shù)解,求實(shí)數(shù)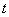 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年高中數(shù)學(xué)全國(guó)各省市理科導(dǎo)數(shù)精選22道大題練習(xí)卷(解析版) 題型:解答題
已知函數(shù)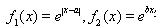
(I)若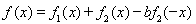 ,是否存在a,b
,是否存在a,b R,y=f(x)為偶函數(shù).如果存在.請(qǐng)舉例并證明你的結(jié)論,如果不存在,請(qǐng)說(shuō)明理由;
R,y=f(x)為偶函數(shù).如果存在.請(qǐng)舉例并證明你的結(jié)論,如果不存在,請(qǐng)說(shuō)明理由;
〔II)若a=2,b=1.求函數(shù)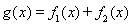 在R上的單調(diào)區(qū)間;
在R上的單調(diào)區(qū)間;
(III )對(duì)于給定的實(shí)數(shù)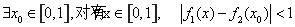 成立.求a的取值范圍.
成立.求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年陜西省咸陽(yáng)市高考模擬考試(一)理科數(shù)學(xué)試卷(解析版) 題型:填空題
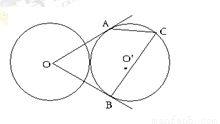
如圖,兩個(gè)等圓⊙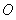 與⊙
與⊙ 外切,過(guò)
外切,過(guò) 作⊙
作⊙ 的兩條切線
的兩條切線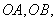
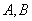 是切點(diǎn),點(diǎn)
是切點(diǎn),點(diǎn)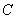 在圓
在圓 上且不與點(diǎn)
上且不與點(diǎn)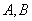 重合,則
重合,則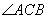 = .
= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年陜西省咸陽(yáng)市高考模擬考試(一)理科數(shù)學(xué)試卷(解析版) 題型:選擇題
設(shè)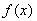 的定義域?yàn)?/span>D,若
的定義域?yàn)?/span>D,若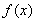 滿足條件:存在
滿足條件:存在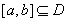 ,使
,使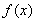 在
在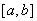 上的值域是
上的值域是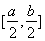 ,則稱(chēng)
,則稱(chēng)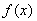 為“倍縮函數(shù)”.若函數(shù)
為“倍縮函數(shù)”.若函數(shù)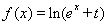 為“倍縮函數(shù)”,則t的范圍是( )
為“倍縮函數(shù)”,則t的范圍是( )
A . 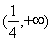 B.
B.  C.
C. 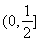 D.
D. 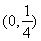
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年廣東省廣州市畢業(yè)班綜合測(cè)試一理科數(shù)學(xué)試卷(解析版) 題型:填空題
在極坐標(biāo)系中,直線 與曲線
與曲線 相交于
相交于 、
、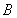 兩點(diǎn),若
兩點(diǎn),若 ,則實(shí)數(shù)
,則實(shí)數(shù) 的值為 .
的值為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2013-2014學(xué)年(安徽專(zhuān)用)高考數(shù)學(xué)(文)仿真模擬卷2練習(xí)卷(解析版) 題型:填空題
已知F1,F2是雙曲線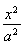 -y2=1的兩個(gè)焦點(diǎn),點(diǎn)P在此雙曲線上,
-y2=1的兩個(gè)焦點(diǎn),點(diǎn)P在此雙曲線上,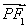 ·
·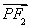 =0,如果點(diǎn)P到x軸的距離等于
=0,如果點(diǎn)P到x軸的距離等于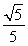 ,那么該雙曲線的離心率等于________.
,那么該雙曲線的離心率等于________.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com