
①截y軸所得弦長為2;
②被x軸分成兩段圓弧,其弧長的比為3∶1.
在滿足條件①②的所有圓中,求圓心到直線l:x-2y=0的距離最小的圓的方程.
思路分析:可設所求圓的標準方程為(x-a)2+(y-b)2=r2,它有三個待定系數a、b、r.將條件②等價轉化為所截圓弧所對的圓心角的度數為90°,進而可求出r與b的關系.將條件①等價轉化為r與a的關系.最后利用算術平均值不等式或方程有實數解的條件:判別式不小于0等方法求出a、b、r.
解法一:設圓的圓心坐標為P(a,b),半徑為r,
則點P到x軸、y軸的距離分別為|b|、|a|.
由題設知圓P截x軸所得劣弧的圓心角為90°,
于是圓P截x軸所得弦長為![]() r,
r,
故r2=2b2.
又圓P截y軸所得的弦長為2,
所以有r2=a2+1,
從而得2b2-a2=1.
點P(a,b)到直線x-2y=0的距離為d=![]() .
.
所以5d2=|a-2b|2=a2+4b2-4ab=2a2+2b2-4ab+1=2(a-b)2+1≥1,
當且僅當a=b時,上式取等號,
此時5d2=1,從而d取得最小值.
由此有
解此方程組得![]()
由r2=2b2,知r2=2.
故所求圓的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2.
解法二:同解法一得d=![]() ,
,
故a-2b=±![]() d.
d.
于是a2=4b2±![]() bd+5d2,①
bd+5d2,①
將a2=2b2-1代入①式,
整理得2b2±![]() db+5d2+1=0.②
db+5d2+1=0.②
把它看作關于b的一元二次方程,由于方程有實根,
故判別式非負,
于是Δ=8(5d2-1)≥0,
解得5d2≥1.
所以5d2有最小值1,從而d有最小值![]() .
.
將其代入②式得2b2±4b+2=0,
解得b=±1.
將b=±1代入r2=2b2,得r2=2.
又由r2=a2+1,得a=±1.
綜上,解得a=±1,b=±1,r2=2.
由|a-2b|=1,知a、b同號.
于是,所求圓的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2.
綠色通道:解題的過程就是實現條件向結論轉化的過程.對于直線與圓,需要綜合平面幾何、解析幾何、代數知識,將條件轉化成熟悉的形式,以便用常規的解題思路求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| QM |
| QP |
查看答案和解析>>
科目:高中數學 來源: 題型:
 在A、B、C、D四小題中只能選做2題,每小題10分,共計20分,請在答題紙指定區域內作答,解答應寫出文字說明、證明過程或演算步驟.
在A、B、C、D四小題中只能選做2題,每小題10分,共計20分,請在答題紙指定區域內作答,解答應寫出文字說明、證明過程或演算步驟.1 1 |
| 2 |
| π |
| 4 |
|
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
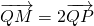 的點M的軌跡為曲線C.
的點M的軌跡為曲線C.查看答案和解析>>
科目:高中數學 來源:2011年湖北省黃岡市高考數學交流試卷3(文科)(解析版) 題型:解答題
 的點M的軌跡為曲線C.
的點M的軌跡為曲線C.查看答案和解析>>
科目:高中數學 來源:2011年湖北省黃岡市高考數學交流試卷(文科)(解析版) 題型:解答題
 的點M的軌跡為曲線C.
的點M的軌跡為曲線C.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com