
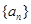 和
和 滿足:
滿足: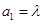 ,
,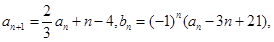 其中
其中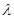 為實數,
為實數,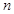 為正整數.
為正整數.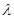 ,證明數列
,證明數列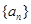 不是等比數列;
不是等比數列;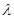 ,試求數列
,試求數列 的前
的前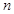 項和
項和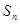 ;
;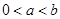 ,是否存在實數
,是否存在實數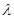 ,使得對任意正整數
,使得對任意正整數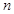 ,都有
,都有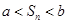 成立? 若存在,求
成立? 若存在,求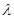 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.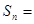
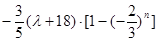
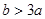 存在實數
存在實數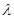 ,
,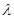 的取值范圍是
的取值范圍是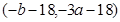
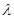 ,使
,使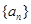 是等比數列,由題意知
是等比數列,由題意知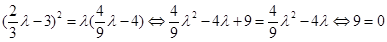 ,矛盾,所以不是等比數列.
,矛盾,所以不是等比數列.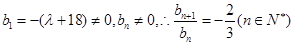 ,故當
,故當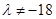 時,數列
時,數列 是以
是以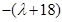 為首項,
為首項,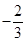 為公比的等比數列.
為公比的等比數列.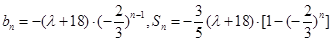 ,由此入手能夠推出存在實數,使得任意正整數n,都有
,由此入手能夠推出存在實數,使得任意正整數n,都有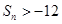 ,
,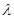 的取值范圍為
的取值范圍為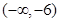 .
.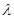 ,使{
,使{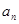 }是等比數列,
}是等比數列,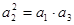 ,
,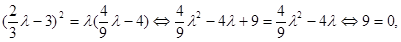 矛盾.
矛盾.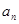 }不是等比數列. ………………………4分
}不是等比數列. ………………………4分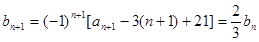
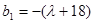 ,所以
,所以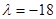 ,
,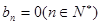 ,此時
,此時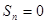
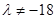 時,
時,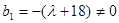 ,
,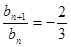
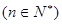 ,
,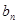 }是以
}是以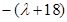 為首項,
為首項,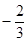 為公比的等比數列.
為公比的等比數列.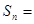
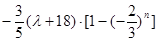 ……………………8分
……………………8分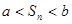 對任意正整數
對任意正整數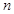 成立,
成立,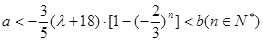
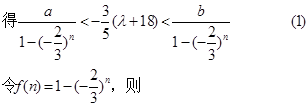
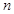 為正奇數時,
為正奇數時,
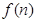 的最大值為
的最大值為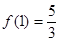 ,
, 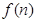 的最小值為
的最小值為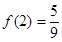 ,
,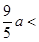
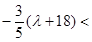
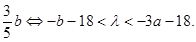
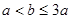 時,由
時,由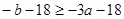 ,不存在實數滿足題目要求;
,不存在實數滿足題目要求;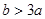 存在實數
存在實數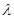 ,使得對任意正整數
,使得對任意正整數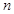 ,都有
,都有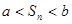 ,且
,且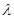 的取值范圍是
的取值范圍是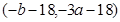 …………………………12分
…………………………12分 

 ABC考王全優卷系列答案
ABC考王全優卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com