
已知數列 的各項都是正數,且對任意
的各項都是正數,且對任意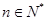 都有
都有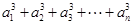
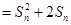 ,其中
,其中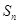 為數列
為數列 的前
的前 項和.
項和.
(1)求 、
、 ;
;
(2)求數列 的通項公式;
的通項公式;
(3)設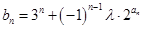 ,對任意的
,對任意的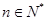 ,都有
,都有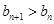 恒成立,求實數
恒成立,求實數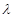 的取值范圍.
的取值范圍.
(1)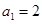 ,
,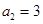 ;(2)
;(2)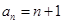 ;(3)
;(3)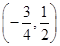 .
.
解析試題分析:(1)分別令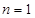 和
和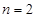 代入題干中的等式求出
代入題干中的等式求出 和
和 的值;(2)利用定義法進行求解,在原式中利用
的值;(2)利用定義法進行求解,在原式中利用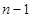 替換
替換 得到
得到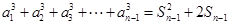 ,將此等式與原式作差得到
,將此等式與原式作差得到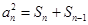
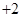 ,再次利用定義法得到數列
,再次利用定義法得到數列 為等差數列,最后利用等差數列的通項公式進行求解;(3)利用
為等差數列,最后利用等差數列的通項公式進行求解;(3)利用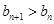 化簡得到
化簡得到 ,對
,對 進行分奇偶討論求出
進行分奇偶討論求出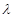 的取值范圍.
的取值范圍.
試題解析:(1)令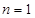 ,則
,則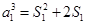 ,即
,即 ,所以
,所以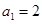 或
或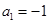 或
或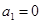 ,
,
又因為數列 的各項都是正數,所以
的各項都是正數,所以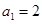 ,
,
令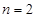 ,則
,則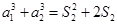 ,即
,即 ,解得
,解得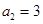 或
或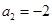 或
或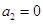 ,
,
又因為數列 的各項都是正數,所以
的各項都是正數,所以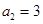 ,
,
(2)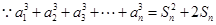 , ①
, ① , ②
, ②
由①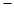 ②得
②得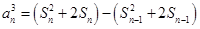 ,
,
化簡得到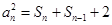 , ③
, ③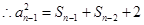 ,④
,④
由③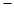 ④得
④得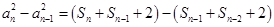 ,
,
化簡得到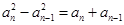 ,即
,即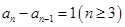 ,
,
當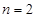 時,
時,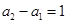 ,所以
,所以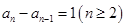 ,
,
所以數列 是一個以
是一個以 為首項,
為首項, 為公差的等差數列,
為公差的等差數列,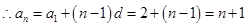 ;
;
(3)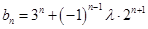 ,
,
因為對任意的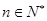 ,都有
,都有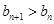 恒成立,即有
恒成立,即有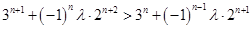 ,
,
化簡得 ,
,
當 為奇數時,
為奇數時, 恒成立,
恒成立, ,即
,即 ,
,
當 為偶數時,
為偶數時,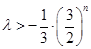 恒成立,
恒成立,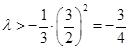 ,即
,即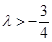 ,
,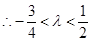 ,故實數
,故實數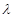 的取值范圍是
的取值范圍是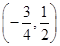 .
.
考點:1.定義法求數列的通項公式;2.數列不等式恒成立;3.分類討論


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案科目:高中數學 來源: 題型:填空題
《萊因德紙草書》(Rhind Papyrus)是世界上最古老的數學著作之一。書中有一道這樣的題目:把100個面包分給五人,使每人成等差數列,且使最大的三份之和的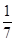 是較小的兩份之和,則最小1份的大小是
是較小的兩份之和,則最小1份的大小是
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列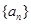 的前
的前 項和
項和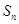 和通項
和通項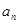 滿足
滿足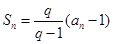 (
(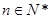 ,
,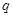 是大于0的常數,且
是大于0的常數,且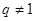 ),數列
),數列 是公比不為
是公比不為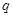 的等比數列,
的等比數列,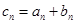 .
.
(1)求數列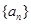 的通項公式;
的通項公式;
(2)設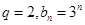 ,是否存在實數
,是否存在實數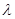 ,使數列
,使數列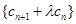 是等比數列?若存在,求出所有可能的實數
是等比數列?若存在,求出所有可能的實數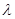 的值,若不存在說明理由;
的值,若不存在說明理由;
(3)數列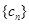 是否能為等比數列?若能,請給出一個符合的條件的
是否能為等比數列?若能,請給出一個符合的條件的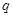 和
和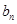 的組合,若不能,請說明理由.
的組合,若不能,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設項數均為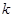 (
(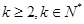 )的數列
)的數列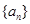 、
、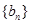 、
、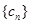 前
前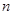 項的和分別為
項的和分別為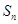 、
、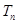 、
、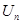 .已知集合
.已知集合 =
=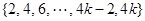 .
.
(1)已知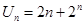 ,求數列
,求數列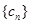 的通項公式;
的通項公式;
(2)若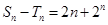
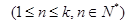 ,試研究
,試研究 和
和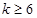 時是否存在符合條件的數列對(
時是否存在符合條件的數列對(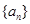 ,
,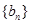 ),并說明理由;
),并說明理由;
(3)若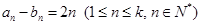 ,對于固定的
,對于固定的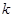 ,求證:符合條件的數列對(
,求證:符合條件的數列對(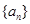 ,
,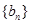 )有偶數對.
)有偶數對.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分18分) 本題共有3個小題,第1小題滿分4分,第2小題滿分6分. 第3小題滿分8分.
(文)對于數列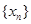 ,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為
,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為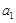 ,公差為
,公差為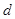 的無窮等差數列
的無窮等差數列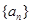 的子數列問題,為此,他取了其中第一項
的子數列問題,為此,他取了其中第一項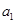 ,第三項
,第三項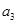 和第五項
和第五項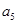 .
.
(1) 若 成等比數列,求
成等比數列,求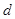 的值;
的值;
(2) 在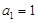 ,
, 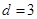 的無窮等差數列
的無窮等差數列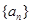 中,是否存在無窮子數列
中,是否存在無窮子數列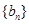 ,使得數列
,使得數列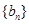 為等比數列?若存在,請給出數列
為等比數列?若存在,請給出數列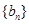 的通項公式并證明;若不存在,說明理由;
的通項公式并證明;若不存在,說明理由;
(3) 他在研究過程中猜想了一個命題:“對于首項為正整數 ,公比為正整數
,公比為正整數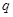 (
(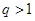 )的無窮等比數 列
)的無窮等比數 列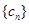 ,總可以找到一個子數列
,總可以找到一個子數列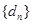 ,使得
,使得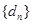 構成等差數列”. 于是,他在數列
構成等差數列”. 于是,他在數列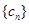 中任取三項
中任取三項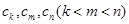 ,由
,由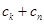 與
與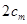 的大小關系去判斷該命題是否正確. 他將得到什么結論?
的大小關系去判斷該命題是否正確. 他將得到什么結論?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com