
(06年山東卷文)(12分)
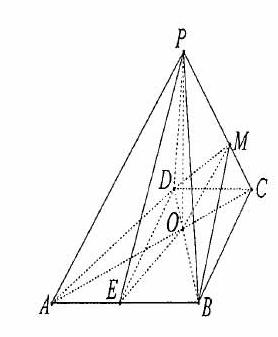
如圖,已知四棱錐P-ABCD的底面ABCD為等腰梯形,AB∥DC,AC⊥BD,AC與BD相交于點(diǎn)O,且頂點(diǎn)P在底面上的射影恰為O點(diǎn),又BO=2,PO=![]() ,PB⊥PD.
,PB⊥PD.
(Ⅰ)求異面直接PD與BC所成角的余弦值;
(Ⅱ)求二面角P-AB-C的大小;
(Ⅲ)設(shè)點(diǎn)M在棱PC上,且![]() 為何值時(shí),PC⊥平面BMD.
為何值時(shí),PC⊥平面BMD.

解析:解法一:
![]() 平面
平面![]() ,
, ![]()
又![]() ,
,
由平面幾何知識(shí)得:![]()
(Ⅰ)過(guò)![]() 做
做![]() 交于
交于![]() 于
于![]() ,連結(jié)
,連結(jié)![]() ,則
,則![]() 或其補(bǔ)角為異面直線
或其補(bǔ)角為異面直線![]() 與
與![]() 所成的角,
所成的角,
![]() 四邊形
四邊形![]() 是等腰梯形,
是等腰梯形,![]()
![]()
又![]() ,
,![]() 四邊形
四邊形![]() 是平行四邊形。
是平行四邊形。
![]() ,
,![]() 是
是![]() 的中點(diǎn),且
的中點(diǎn),且![]()
又![]() ,
,![]() 為直角三角形,
為直角三角形,
![]()
在![]() 中,由余弦定理得
中,由余弦定理得
![]()
故異面直線PD與![]() 所成的角的余弦值為
所成的角的余弦值為![]()
(Ⅱ)連結(jié)![]() ,由(Ⅰ)及三垂線定理知,
,由(Ⅰ)及三垂線定理知,![]() 為二面角
為二面角![]() 的平面角
的平面角
![]() ,
,![]()
![]() 二面角
二面角![]() 的大小為
的大小為![]()
(Ⅲ)連結(jié)![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() ,又在
,又在![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,故
,故![]() 時(shí),
時(shí),![]() 平面
平面![]()
解法二: ![]() 平面
平面![]() ,
,![]()
又![]() ,
,![]() ,
,
由平面幾何知識(shí)得:![]()
以![]() 為原點(diǎn),
為原點(diǎn),![]() 分別為
分別為![]() 軸建立如圖所示的空間直角坐標(biāo)系,
軸建立如圖所示的空間直角坐標(biāo)系,

則各點(diǎn)坐標(biāo)為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(Ⅰ)![]() ,
,![]() ,
,
![]() 。
。
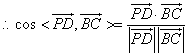
![]() 。
。
故直線![]() 與
與![]() 所成的角的余弦值為
所成的角的余弦值為![]()
(Ⅱ)設(shè)平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() ,
,
由于![]() ,
,![]() ,
,
由 得
得 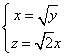
取![]() ,又已知平面ABCD的一個(gè)法向量
,又已知平面ABCD的一個(gè)法向量![]() ,
,
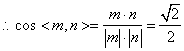
又二面角![]() 為銳角,
為銳角,
![]() 所求二面角
所求二面角![]() 的大小為
的大小為![]()
(Ⅲ)設(shè)![]() ,由于
,由于![]() 三點(diǎn)共線,
三點(diǎn)共線,![]() ,
,
![]() 平面
平面![]() ,
,
![]()
![]()
![]()
由(1)(2)知:![]() ,
,![]() 。
。
![]() ,
,![]()
故![]() 時(shí),
時(shí),![]() 平面
平面![]() 。
。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com