
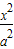 +
+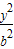 =1(a>b>0)的兩個焦點為F1、F2,短軸兩端點B1、B2,已知F1、F2、B1、B2四點共圓,且點N(0,3)到橢圓上的點最遠距離為5
=1(a>b>0)的兩個焦點為F1、F2,短軸兩端點B1、B2,已知F1、F2、B1、B2四點共圓,且點N(0,3)到橢圓上的點最遠距離為5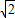 .
.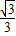 )、Q的直線對稱?若能,求出k的取值范圍;若不能,請說明理由.
)、Q的直線對稱?若能,求出k的取值范圍;若不能,請說明理由.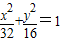 .由直線l與橢圓相交于不同的兩點可得△>0即m2<32k2+16,要使A、B兩點關于過點P、Q的直線對稱,必須
.由直線l與橢圓相交于不同的兩點可得△>0即m2<32k2+16,要使A、B兩點關于過點P、Q的直線對稱,必須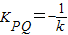 ,利用方程的根與系數的關系代入得
,利用方程的根與系數的關系代入得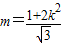 ,從而可求k得范圍
,從而可求k得范圍 ,N(0,3)
,N(0,3)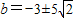 (舍去),
(舍去),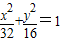 .
.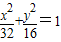 得(1+2k2)x2+4kmx+(2m2-32)=0.
得(1+2k2)x2+4kmx+(2m2-32)=0.
 ,
,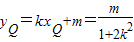

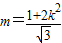 .③
.③
 ,
,
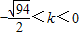 或0
或0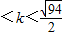
 或0
或0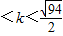 時,A、B兩點關于過點P、Q的直線對稱.
時,A、B兩點關于過點P、Q的直線對稱.

科目:高中數學 來源: 題型:
設F1、F2分別為橢圓C:![]() =1(a>b>0)的左、右兩個焦點.
=1(a>b>0)的左、右兩個焦點.
(1)若橢圓C上的點A(1,![]() )到F1、F2兩點的距離之和等于4,寫出橢圓C的方程和焦點坐標;
)到F1、F2兩點的距離之和等于4,寫出橢圓C的方程和焦點坐標;
(2)設點P是(1)中所得橢圓上的動點,當P在何位置時,![]() 最大,說明理由,并求出最大值。
最大,說明理由,并求出最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:
設F1、F2分別為橢圓C:![]() =1(a>b>0)的左、右兩個焦點.
=1(a>b>0)的左、右兩個焦點.
(1)若橢圓C上的點A(1,![]() )到F1、F2兩點的距離之和等于4,寫出橢圓C的方程和焦點坐標;
)到F1、F2兩點的距離之和等于4,寫出橢圓C的方程和焦點坐標;
(2)設點K是(1)中所得橢圓上的動點,求線段F1K的中點的軌跡方程;
查看答案和解析>>
科目:高中數學 來源:2011年高考數學總復習備考綜合模擬試卷(3)(解析版) 題型:解答題
 +
+ =1(a>b>0),直線l為圓O:x2+y2=b2的一條切線,記橢圓C的離心率為e.
=1(a>b>0),直線l為圓O:x2+y2=b2的一條切線,記橢圓C的離心率為e. ,且恰好經過橢圓的右頂點,求e的大小;
,且恰好經過橢圓的右頂點,求e的大小; y+3=0相切,求橢圓方程.
y+3=0相切,求橢圓方程.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣西桂林市、崇左市、防城港市高考第一次聯合模擬理科數學試卷(解析版) 題型:解答題
如圖,已知橢圓C: +
+ =1(a>b>0)的左、右焦點分別為F
=1(a>b>0)的左、右焦點分別為F 、F
、F ,A是橢圓C上的一點,AF
,A是橢圓C上的一點,AF ⊥F
⊥F F
F ,O是坐標原點,OB垂直AF
,O是坐標原點,OB垂直AF 于B,且OF
于B,且OF =3OB.
=3OB.

(Ⅰ)求橢圓C的離心率;
(Ⅱ)求t∈(0,b),使得命題“設圓x +y
+y =t
=t 上任意點M(x
上任意點M(x ,y
,y )處的切線交橢圓C于Q
)處的切線交橢圓C于Q 、Q
、Q 兩點,那么OQ
兩點,那么OQ ⊥OQ
⊥OQ ”成立.
”成立.
查看答案和解析>>
科目:高中數學 來源:2010年遼寧省沈陽四校聯合體高二上學期期中考試理科數學卷 題型:選擇題
設F1、F2分別為橢圓C: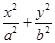 =1(a>b>0)的左、右焦點.
=1(a>b>0)的左、右焦點.
(Ⅰ)若橢圓上的點A(1,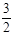 )到點F1、F2的距離之和等于4,求橢圓C的方程;
)到點F1、F2的距離之和等于4,求橢圓C的方程;
(Ⅱ)設點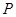 是(Ⅰ)中所得橢圓C上的動點,求線段
是(Ⅰ)中所得橢圓C上的動點,求線段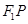 的中點
的中點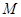 的軌跡方程.
的軌跡方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com