
有4名同學參加唱歌、跳舞、下棋三項比賽,每項比賽至少有1人參加,每名同學只參加一項比賽,另外甲同學不能參加跳舞比賽,則不同的參賽方案的種數為_____(用數字作答).
24
解析試題分析:因為將4名學生參加三項比賽,那么每項比賽至少有1人參加,則將4=1+1+2,同時由于甲同學不能參加跳舞比賽,因此可以分為兩類,參加跳舞的只有一個人時,那么先選出一個人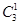 ,然后將其與的三個人分組為3=1+2,所有的情況有
,然后將其與的三個人分組為3=1+2,所有的情況有 ,利用分步乘法計數原理得到為
,利用分步乘法計數原理得到為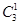
 =18種,同時參加跳舞的有兩個人時,則有
=18種,同時參加跳舞的有兩個人時,則有 ,剩余的參加的比賽分組分配有
,剩余的參加的比賽分組分配有 ,利用乘法計數原理可知共有
,利用乘法計數原理可知共有
 =6,結合分類計數加法原理得到為18+6=24,因此填寫24.
=6,結合分類計數加法原理得到為18+6=24,因此填寫24.
考點:本試題考查了排列組合的運用。
點評:解決該試題的關鍵是利用已知的條件,能合理的運用分組的思想來分配人員,同時能對于特殊元素優先考慮的思想來解答,屬于中檔題。


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:填空題
現將10個扶貧款的名額分配給某鄉鎮不同的四個村,要求一個村1個名額,一個村2個名額,一個村3個名額,一個村4個名額,則不同的分配方案種數為 .
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
用1、2、3、4、5、6、7、8組成沒有重復數字的八位數,要求1與2 相鄰,3與4相鄰,5與6相鄰,而7與8不相鄰,這樣的八位數共有 個.(用數字作答)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
規定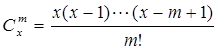 ,其中
,其中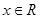 ,
, 是正整數,且
是正整數,且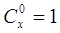 ,這是組合數
,這是組合數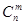 (
( 、
、 是正整數,且
是正整數,且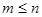 )的一種推廣.如當
)的一種推廣.如當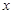 =-5時,
=-5時,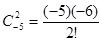
(1)求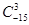 的值;
的值;
(2)設x>0,當x為何值時,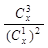 取得最小值?
取得最小值?
(3)組合數的兩個性質;
①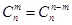 . ②
. ② .
.
是否都能推廣到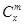 (
(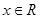 ,
, 是正整數)的情形?若能推廣,則寫出推廣的形式并給出證明;若不能,則說明理由.
是正整數)的情形?若能推廣,則寫出推廣的形式并給出證明;若不能,則說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com