Question

k取何值時，方程7x²-（k+13）x+k²-k-2=0的兩個根分別在（0，1）和（1，2）內．

Answer 1

解：記f（x）=7x²-（k+13）x+k²-k-2，由題意可得 ，
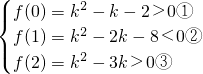
解①得 k＜-1，或 k＞2．
解②得 k＜-2，或 k＞6．
解③得 k＜0，或k＞3．
把①②③的解集取交集可得 {k|k＜-2，或 k＞6}，
故k的取值范圍為 {k|k＜-2，或 k＞6}．
分析：記f（x）=7x²-（k+13）x+k²-k-2，由題意可得f（0）＞0，f（1）＜0，f（2）＞0，解由這三個不等式組成的不等式組，求得k的取值范圍．
點評：本題主要考查函數零點的判定定理，考查二次函數與不等式組，難度適中，關鍵是根據已知條件列出不等式組進行求解，屬于基礎題．