
(12分)已知拋物線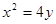 的焦點為
的焦點為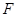 ,準線為
,準線為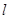 ,過
,過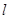 上一點P作拋物線的兩切線,切點分別為A、B,
上一點P作拋物線的兩切線,切點分別為A、B,
(1)求證: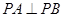 ;
;
(2)求證:A、F、B三點共線;
(3)求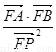 的值.
的值.
(3)
【解析】
試題分析:(1)準線為y=-1,F(0,1),設P(n,-1),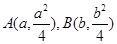 ,
,
因為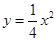 ,所以
,所以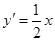 ,
,
所以 ,即
,即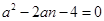 ,
,
 ,即
,即 ,
,
所以a,b是方程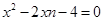 ,
,
所以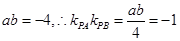 ,
,
所以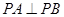 .
.
(2)由(1)知a+b=2n,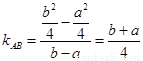 ,
,
所以直線AB的方程為 即
即
因為a+b=2n,ab=-4,所以直線AB的方程為 ,
,
所以恒過點F(0,1).
(3)
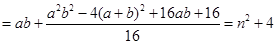 ,
,
因為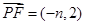 ,所以
,所以 ,
,
所以
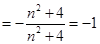 為常數.
為常數.
考點:直線與拋物線的相切,直線的斜率,導數的幾何意義,向量的數量積.
點評:根據導數的幾何意義,分別求出切點A,B處的導數即A,B的斜率,然后證明斜率之積為-1,來證明兩條切線垂直.證明A,B,F三點共線,關鍵是利用第(1)問的結果,求出AB的點方程,證明點F的坐標滿足此方程即可.第(3)問分別求出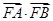 和
和 都用n表示,從而證明其為定值.
都用n表示,從而證明其為定值.


科目:高中數學 來源:2013-2014學年浙江省高三上學期第三次統練理科數學試卷(解析版) 題型:解答題
已知拋物線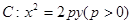 的焦點為
的焦點為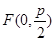 ,準線為
,準線為 ,點
,點 為拋物線C上的一點,且
為拋物線C上的一點,且 的外接圓圓心到準線的距離為
的外接圓圓心到準線的距離為 .
.

(I)求拋物線C的方程;
(II)若圓F的方程為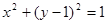 ,過點P作圓F的2條切線分別交
,過點P作圓F的2條切線分別交 軸于點
軸于點 ,求
,求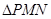 面積的最小值時
面積的最小值時 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年浙江省臺州市高三調研考試理數 題型:選擇題
已知拋物線 的焦點為
的焦點為 ,
, 關于原點的對稱點為
關于原點的對稱點為 過
過 作
作 軸的垂線交拋物線于
軸的垂線交拋物線于 兩點.有下列四個命題:①
兩點.有下列四個命題:① 必為直角三角形;②
必為直角三角形;② 不一定為直角三角形;③直線
不一定為直角三角形;③直線 必與拋物線相切;④直線
必與拋物線相切;④直線 不一定與拋物線相切.其中正確的命題是
不一定與拋物線相切.其中正確的命題是
(A)①③ (B)①④ (C)②③ (D)②④
查看答案和解析>>
科目:高中數學 來源:2010-2011年黑龍江省高二上學期期末考試數學理卷 題型:選擇題
已知拋物線 的焦點為F,準線為
的焦點為F,準線為 ,經過F且斜率為
,經過F且斜率為 的直線與拋物線在
的直線與拋物線在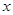 軸上方的部分相交于點A,且AK
軸上方的部分相交于點A,且AK
 ,垂足為K,則
,垂足為K,則 的面積是( )
的面積是( )
A 4 B  C
C  D 8
D 8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com