甲、乙、丙三人獨立破譯同一份密碼，已知甲、乙、丙各自破譯出密碼的概率分別為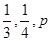
，
且他們是否破譯出密碼互不影響，若三人中只有甲破譯出密碼的概率為
.
（1）求
的值，
(2）設在甲、乙、丙三人中破譯出密碼的總人數為X，求X的分布列和數學期望E（X）.
（1）
；（2）分布列詳見解析，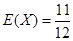
.
解析試題分析：本題主要考查概率的計算公式、事件的相互獨立性、離散型隨機變量的分布列與數學期望等基礎知識，考查運用概率知識解決簡單實際問題的能力，考查基本運算能力.第一問，是事件的相互獨立性，通過獨立事件的概率公式列出已知條件中的表達式，解方程解出
；第二問，是求分布列和期望，同樣利用獨立事件的概率公式，求出每一種情況下的概率，畫出分布列，利用期望的計算公式計算期望.
試題解析：記“甲、乙、丙三人各自破譯出密碼”分別為事件
，依題意有
，
，且相互獨立. 2分
（1）設“三人中只有甲破譯出密碼”為事件
，
則有
. 5分
所以
，得. 6分
（2）
的所有可能取值為0,1,2,3.
所以
，
，
，
. 10分的分布列為
所以
. 12分
考點：1.獨立事件的概率；2.分布列；3.期望.
科目：高中數學 來源： 題型：解答題
某公司招聘員工采取兩次考試(筆試)的方法：第一試考選擇題，共10道題（均為四選一題型），每題10分，共100分；第二試考解答題，共3題。規則是：只有在一試中達到或超過80分者才獲通過并有資格參加二試，參加二試的人只有答對2題或3題才能被錄用。現有甲、乙兩人參加該公司的招聘考試。且已知在一試時：兩人均會做10道題中的6道；對于另外4道題來說，甲有兩題可排除兩個錯誤答案、有兩題完全要猜，乙有兩題可排除一個錯誤答案、有一題可排除兩個錯誤答案、有一題完全要猜。進入二試后，對于任意一題，甲答對的概率是
、乙答對的概率是
.（1）分別求甲、乙兩人能通過一試進入二試的概率
、
；（2）求甲、乙兩人都能被錄用的概率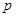
.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某市
、
、
、
四所中學報名參加某高校今年自主招生的學生人數如下表所示：
| 中學 | | | | |
| 人數 |  |  |  |  |
名參加問卷調查．、、、四所中學各抽取多少名學生？名學生中隨機抽取兩名學生，求這兩名學生來自同一所中學的概率；名學生中，從來自、兩所中學的學生當中隨機抽取兩名學生，用
表示抽得中學的學生人數，求的分布列.查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某網站用“10分制”調查一社區人們的幸福度.現從調查人群中隨機抽取16名，以下莖葉圖記錄了他們的幸福度分數（以小數點前的一位數字為莖，小數點后的一位數字為葉）：
（1）若幸福度不低于9.5分，則稱該人的幸福度為“極幸福”，求從這16人隨機選取3人，至多有1人是“極幸福”的概率；
（2）以這16人的樣本數據來估計整個社區的總體數據，若從該社區（人數很多）任選3人，記
表示抽到“極幸福”的人數，求的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
一個盒子中裝有分別標有數字1、2、3、4的4個大小、形狀完全相同的小球，現從中有放回地隨機抽取2個小球，抽取的球的編號分別記為
、
，記
.
（Ⅰ）求
取最大值的概率；
（Ⅱ）求的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
甲，乙，丙三位學生獨立地解同一道題，甲做對的概率為
，乙，丙做對的概率分別為
，
(＞)，且三位學生是否做對相互獨立.記
為這三位學生中做對該題的人數，其分布列為：
| 0 | 1 | 2 | 3 |
 |  |  |  |  |
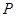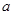，的值；的數學期望.查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（12分）一個盒子中裝有4張卡片，每張卡片上寫有1個數字，數字分別是1、2、3、4，現從盒子中隨機抽取卡片.
(Ⅰ)若一次從中隨機抽取3張卡片，求3張卡片上數字之和大于或等于7的概率；
(Ⅱ)若第一次隨機抽取1張卡片，放回后再隨機抽取1張卡片，求兩次抽取的卡片中至少一次抽到數字2的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分12分）
一個不透明的袋子中裝有4個形狀相同的小球，分別標有不同的數字2，3，4，
，現從袋中隨機摸出2個球，并計算摸出的這2個球上的數字之和，記錄后將小球放回袋中攪勻，進行重復試驗。記A事件為“數字之和為7”.試驗數據如下表
| 摸球總次數 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和為7”出現的頻數 | 1 | 9 | 14 | 24 | 26 | 37 | 58 | 82 | 109 | 150 |
| “和為7”出現的頻率 | 0.10 | 0.45 | 0.47 | 0.40 | 0.29 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
）的值； 
元，求的數學期望和方差。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
為選取女生的人數，求X的分布列及數學期望．