
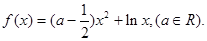
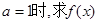 在區間
在區間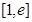 上的最大值和最小值;
上的最大值和最小值;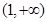 上,函數
上,函數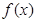 的圖象恒在直線
的圖象恒在直線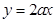 下方,求
下方,求 的取值范圍.
的取值范圍.科目:高中數學 來源:不詳 題型:解答題
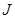 型卡車將某種水果運送(滿載)到相距400km的水果批發市場.據測算,
型卡車將某種水果運送(滿載)到相距400km的水果批發市場.據測算,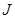 型卡車滿載行駛時,每100km所消耗的燃油量
型卡車滿載行駛時,每100km所消耗的燃油量 (單位:
(單位: )與速度
)與速度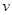 (單位:km/h)的關系近似地滿足
(單位:km/h)的關系近似地滿足 ,除燃油費外,人工工資、車損等其他費用平均每小時300元.已知燃油價格為7.5元/L.
,除燃油費外,人工工資、車損等其他費用平均每小時300元.已知燃油價格為7.5元/L.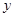 (元)(不計返程費用),將
(元)(不計返程費用),將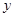 表示成速度
表示成速度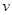 的函數關系式;
的函數關系式;查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 的圖象與
的圖象與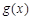 的圖象關于直線
的圖象關于直線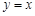 對稱。
對稱。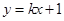 與
與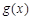 的圖像相切, 求實數
的圖像相切, 求實數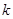 的值;
的值;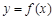 與曲線
與曲線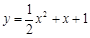 公共點的個數.
公共點的個數.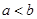 ,比較
,比較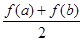 與
與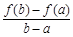 的大小, 并說明理由.
的大小, 并說明理由. 查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.b>a>c | B.c>a>b |
| C.c>b>a | D.a>c>b |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com