
理科(本小題14分)已知函數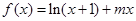 ,當
,當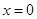 時,函數
時,函數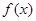 取得極大值.
取得極大值.
(Ⅰ)求實數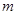 的值;(Ⅱ)已知結論:若函數
的值;(Ⅱ)已知結論:若函數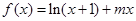 在區間
在區間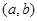 內導數都存在,且
內導數都存在,且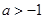 ,則存在
,則存在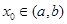 ,使得
,使得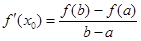 .試用這個結論證明:若
.試用這個結論證明:若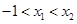 ,函數
,函數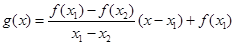 ,則對任意
,則對任意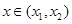 ,都有
,都有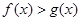 ;(Ⅲ)已知正數
;(Ⅲ)已知正數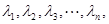 滿足
滿足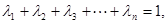 求證:當
求證:當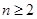 ,
,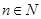 時,對任意大于
時,對任意大于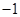 ,且互不相等的實數
,且互不相等的實數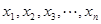 ,都有
,都有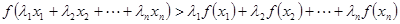
(Ⅰ)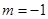 .
.
(Ⅱ)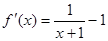
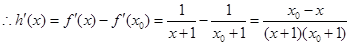
當 時,
時,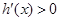 ,
,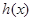 單調遞增,
單調遞增,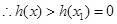 ;
;
當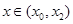 時,
時, ,
,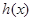 單調遞減,
單調遞減,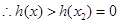 ;(Ⅲ)用數學歸納法證明.
;(Ⅲ)用數學歸納法證明.
【解析】
試題分析:(Ⅰ) . 由
. 由 ,得
,得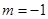 ,此時
,此時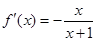 .
.
當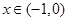 時,
時, ,函數
,函數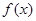 在區間
在區間 上單調遞增;
上單調遞增;
當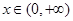 時,
時,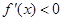 ,函數
,函數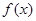 在區間
在區間 上單調遞減.
上單調遞減.
 函數
函數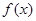 在
在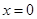 處取得極大值,故
處取得極大值,故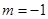 .
3分
.
3分
(Ⅱ)令 , 4分
, 4分
則 .函數
.函數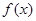 在
在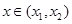 上可導,
上可導,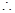 存在
存在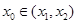 ,使得
,使得 .
.
又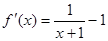

當 時,
時,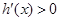 ,
,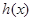 單調遞增,
單調遞增,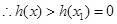 ;
;
當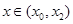 時,
時, ,
,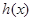 單調遞減,
單調遞減,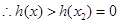 ;
;
故對任意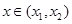 ,都有
,都有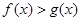 .
8分
.
8分
(Ⅲ)用數學歸納法證明.
①當 時,
時, ,且
,且 ,
,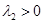 ,
,
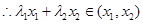 ,
,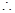 由(Ⅱ)得
由(Ⅱ)得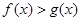 ,即
,即
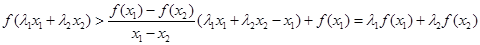 ,
,
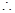 當
當 時,結論成立. 9分
時,結論成立. 9分
②假設當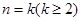 時結論成立,即當
時結論成立,即當 時,
時,
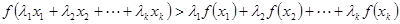 . 當
. 當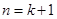 時,設正數
時,設正數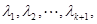 滿足
滿足 令
令 ,
,

則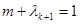 ,且
,且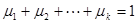 .
.


13分
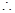 當
當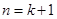 時,結論也成立.
時,結論也成立.
綜上由①②,對任意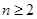 ,
,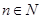 ,結論恒成立. 14分
,結論恒成立. 14分
考點:本題主要考查導數的幾何意義,應用導數研究函數的單調性、最值及不等式的證明,數學歸納法。
點評:難題,利用導數研究函數的單調性、極值、最值,是導數的應用中的基本問題。本題(III)應用數學歸納法證明不等式,難度較大。涉及對數函數,要特別注意函數的定義域。


科目:高中數學 來源: 題型:
(本小題滿分14分)
已知點P ( t , y )在函數f ( x ) = ![]() (x ?? –1)的圖象上,且有t2 – c2at + 4c2 = 0 ( c ?? 0 ).
(x ?? –1)的圖象上,且有t2 – c2at + 4c2 = 0 ( c ?? 0 ).
(1) 求證:| ac | ?? 4;(2) 求證:在(–1,+∞)上f ( x )單調遞增.(3) (僅理科做)求證:f ( | a | ) + f ( | c | ) > 1.
查看答案和解析>>
科目:高中數學 來源:2014屆江西南昌八一、洪都、麻丘中學高二上期中數學試卷(解析版) 題型:解答題
(本小題滿分14分)(理科)已知橢圓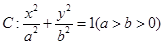 ,過焦點且垂直于長軸的弦長為1,且焦點與短軸兩端點構成等邊三角形.
,過焦點且垂直于長軸的弦長為1,且焦點與短軸兩端點構成等邊三角形.
(1)求橢圓的方程;
(2)過點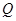
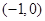 的直線
的直線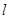 交橢圓于
交橢圓于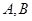 兩點,交直線
兩點,交直線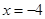 于點
于點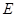 ,且
,且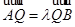 ,
,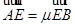 ,
,
求證: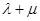 為定值,并計算出該定值.
為定值,并計算出該定值.
查看答案和解析>>
科目:高中數學 來源:2010年廣東省高二上學期期中考試數學卷 題型:解答題
(本小題滿分14分) 已知數列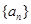 和
和 滿足:
滿足: ,
, ,
, ,
, (
( ),且
),且 是以
是以 為公比的等比數列.
為公比的等比數列.
(Ⅰ)證明: ;
;
(Ⅱ)若 ,證明:數列
,證明:數列 是等比數列;
是等比數列;
(Ⅲ)(理科做,文科不做)若 ,求和:
,求和: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
(2012年高考四川卷理科22) (本小題滿分14分)
已知![]() 為正實數,
為正實數,![]() 為自然數,拋物線
為自然數,拋物線![]() 與
與![]() 軸正半軸相交于點
軸正半軸相交于點![]() ,設
,設![]() 為該拋物線在點
為該拋物線在點![]() 處的切線在
處的切線在![]() 軸上的截距。
軸上的截距。
(Ⅰ)用![]() 和
和![]() 表示
表示![]() ;
;
(Ⅱ)求對所有![]() 都有
都有![]() 成立的
成立的![]() 的最小值;
的最小值;
(Ⅲ)當![]() 時,比較
時,比較![]() 與
與![]() 的大小,并說明理由.
的大小,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com