
設(shè) (
(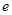 是自然對數(shù)的底數(shù),
是自然對數(shù)的底數(shù),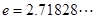 ),且
),且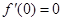 .
.
(1)求實數(shù)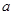 的值,并求函數(shù)
的值,并求函數(shù)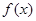 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)設(shè)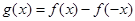 ,對任意
,對任意 ,恒有
,恒有 成立.求實數(shù)
成立.求實數(shù) 的取值范圍;
的取值范圍;
(3)若正實數(shù)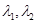 滿足
滿足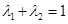 ,
,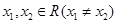 ,試證明:
,試證明: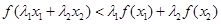 ;并進一步判斷:當(dāng)正實數(shù)
;并進一步判斷:當(dāng)正實數(shù) 滿足
滿足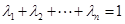
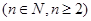 ,且
,且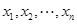 是互不相等的實數(shù)時,不等式
是互不相等的實數(shù)時,不等式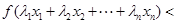
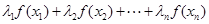 是否仍然成立.
是否仍然成立.
(1)參考解析;(2) ;(3)成立,參考解析
;(3)成立,參考解析
解析試題分析:(1)由 (
(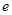 是自然對數(shù)的底數(shù),
是自然對數(shù)的底數(shù),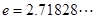 ),且
),且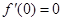 ,即可求出
,即可求出 .再根據(jù)導(dǎo)函數(shù)的值即可求出單調(diào)區(qū)間.
.再根據(jù)導(dǎo)函數(shù)的值即可求出單調(diào)區(qū)間.
(2)對任意 ,恒有
,恒有 成立,通過去分母,整理成兩個函數(shù)的單調(diào)性的問題即
成立,通過去分母,整理成兩個函數(shù)的單調(diào)性的問題即 ,則
,則 在
在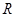 上單調(diào)遞增,又
上單調(diào)遞增,又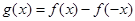 ,再通過求導(dǎo)即可得到m的取值范圍.
,再通過求導(dǎo)即可得到m的取值范圍.
(3)若正實數(shù)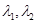 滿足
滿足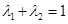 ,
,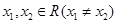 ,則
,則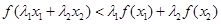 .通過代入函數(shù)關(guān)系式消元再用基本不等式即可得到結(jié)論.當(dāng)
.通過代入函數(shù)關(guān)系式消元再用基本不等式即可得到結(jié)論.當(dāng)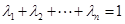
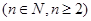 ,且
,且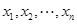 是互不相等的實數(shù)時,不等式
是互不相等的實數(shù)時,不等式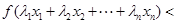
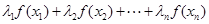 是否仍然成立.有數(shù)學(xué)歸納法證明,當(dāng)n=k+1時利用
是否仍然成立.有數(shù)學(xué)歸納法證明,當(dāng)n=k+1時利用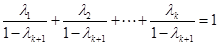 轉(zhuǎn)化為k項的形式.再通過構(gòu)造即可得到結(jié)論.
轉(zhuǎn)化為k項的形式.再通過構(gòu)造即可得到結(jié)論.
(1)∵ ,
, ,故
,故 . 1分
. 1分
令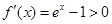 得
得 ;令
;令 得
得 . 3分
. 3分
所以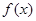 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為 ;單調(diào)遞減區(qū)間為
;單調(diào)遞減區(qū)間為 . 4分
. 4分
(2)由
 變形得:
變形得: . 5分
. 5分
令函數(shù) ,則
,則 在
在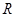 上單調(diào)遞增. 6分
上單調(diào)遞增. 6分 即
即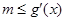 在
在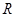 上恒成立. 7分
上恒成立. 7分
而 (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng) 時取“=”)
時取“=”)
所以 . 9分
. 9分
(3)證明:不妨設(shè)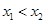 ,由
,由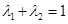
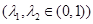 得:
得:
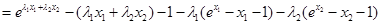
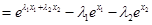
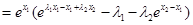


其中 ,故上式的符號由因式“
,故上式的符號由因式“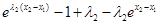 ”的符號確定.
”的符號確定.
令 ,則函數(shù)
,則函數(shù)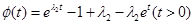 .
. ,其中
,其中 ,得
,得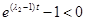 ,故
,故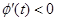 .即
.即 在
在 上單調(diào)遞減,且
上單調(diào)遞減,且 .所以
.所以 .
.
從而有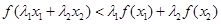 成立.
成立.
該不等式能更進一步推廣:
已知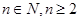 ,
,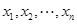 是互不相等的實數(shù),若正實數(shù)
是互不相等的實數(shù),若正實數(shù)


 作業(yè)輔導(dǎo)系列答案
作業(yè)輔導(dǎo)系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
經(jīng)英國相關(guān)機構(gòu)判斷,MH370在南印度洋海域消失.中國兩艦艇隨即在邊長為100海里的某正方形ABCD(如圖)海域內(nèi)展開搜索.兩艘搜救船在A處同時出發(fā),沿直線AP、AQ向前聯(lián)合搜索,且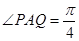 (其中點P、Q分別在邊BC、CD上),搜索區(qū)域為平面四邊形APCQ圍成的海平面.設(shè)
(其中點P、Q分別在邊BC、CD上),搜索區(qū)域為平面四邊形APCQ圍成的海平面.設(shè)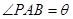 ,搜索區(qū)域的面積為
,搜索區(qū)域的面積為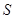 .
.
(1)試建立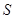 與
與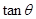 的關(guān)系式,并指出
的關(guān)系式,并指出 的取值范圍;
的取值范圍;
(2)求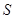 的最大值,并求此時
的最大值,并求此時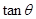 的值.
的值.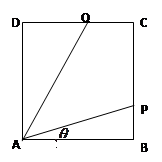
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知定義域為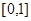 的函數(shù)
的函數(shù) 同時滿足以下三個條件:
同時滿足以下三個條件:
①對任意的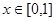 ,總有
,總有 ;
;
②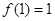 ;
;
③當(dāng)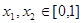 ,且
,且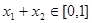 時,
時,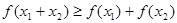 成立.
成立.
稱這樣的函數(shù)為“友誼函數(shù)”.
請解答下列各題:
(1)已知 為“友誼函數(shù)”,求
為“友誼函數(shù)”,求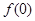 的值;
的值;
(2)函數(shù)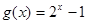 在區(qū)間
在區(qū)間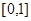 上是否為“友誼函數(shù)”?請給出理由;
上是否為“友誼函數(shù)”?請給出理由;
(3)已知 為“友誼函數(shù)”,假定存在
為“友誼函數(shù)”,假定存在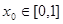 ,使得
,使得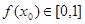 ,且
,且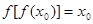 ,求證:
,求證: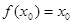 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)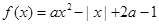 (
( 為實常數(shù)).
為實常數(shù)).
(1)若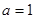 ,求函數(shù)
,求函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)設(shè) 在區(qū)間
在區(qū)間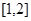 上的最小值為
上的最小值為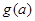 ,求
,求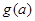 的表達式.
的表達式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某公司為一家制冷設(shè)備廠設(shè)計生產(chǎn)一種長方形薄板,其周長為4米,這種薄板須沿其對角線折疊后使用.如圖所示,ABCD(AB>AD)為長方形薄板,沿AC折疊后,AB′交DC于點P.當(dāng)△ADP的面積最大時最節(jié)能,凹多邊形ACB′PD的面積最大時制冷效果最好.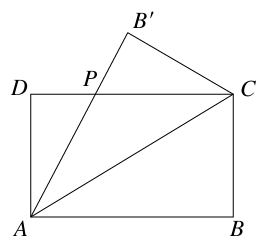
(1)設(shè)AB=x(米),用x表示圖中DP的長度,并寫出x的取值范圍;
(2)若要求最節(jié)能,應(yīng)怎樣設(shè)計薄板的長和寬?
(3)若要求制冷效果最好,應(yīng)怎樣設(shè)計薄板的長和寬?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
對于函數(shù)f(x)若存在x0∈R,f(x0)=x0成立,則稱x0為f(x)的不動點.已知f(x)=ax2+(b+1)x+b-1(a≠0).
(1)當(dāng)a=1,b=-2時,求函數(shù)f(x)的不動點;
(2)若對任意實數(shù)b,函數(shù)f(x)恒有兩個相異的不動點,求a的取值范圍;
(3)在(2)的條件下,若y=f(x)圖象上A,B兩點的橫坐標(biāo)是函數(shù)f(x)的不動點,且A,B兩點關(guān)于直線y=kx+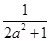 對稱,求b的最小值.
對稱,求b的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(2014·孝感模擬)已知定義在區(qū)間[0,2]上的兩個函數(shù)f(x)和g(x),其中f(x)=-x2+2ax+1+a2,g(x)=x- +
+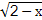 .
.
(1)求函數(shù)f(x)的最小值.
(2)對于?x1,x2∈[0,2],f(x1)>g(x2)恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
為了凈化空氣,某科研單位根據(jù)實驗得出,在一定范圍內(nèi),每噴灑1個單位的凈化劑,空氣中釋放的濃度y(單位:毫克/立方米)隨著時間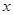 (單位:天)變化的函數(shù)關(guān)系式近似為
(單位:天)變化的函數(shù)關(guān)系式近似為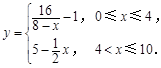 若多次噴灑,則某一時刻空氣中的凈化劑濃度為每次投放的凈化劑在相應(yīng)時刻所釋放的濃度之和.由實驗知,當(dāng)空氣中凈化劑的濃度不低于4(毫克/立方米)時,它才能起到凈化空氣的作用.
若多次噴灑,則某一時刻空氣中的凈化劑濃度為每次投放的凈化劑在相應(yīng)時刻所釋放的濃度之和.由實驗知,當(dāng)空氣中凈化劑的濃度不低于4(毫克/立方米)時,它才能起到凈化空氣的作用.
(1)若一次噴灑4個單位的凈化劑,則凈化時間可達幾天?
(2)若第一次噴灑2個單位的凈化劑,6天后再噴灑a(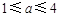 )個單位的藥劑,要使接下來的4天中能夠持續(xù)有效凈化,試求
)個單位的藥劑,要使接下來的4天中能夠持續(xù)有效凈化,試求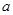 的最小值(精確到0.1,參考數(shù)據(jù):
的最小值(精確到0.1,參考數(shù)據(jù):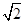 取1.4).
取1.4).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知冪函數(shù)f(x)=x(m2+m)-1(m∈N*),經(jīng)過點(2,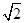 ),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數(shù)a的取值范圍.
),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數(shù)a的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com