

 ;
; ,求AB的長.
,求AB的長. 為正三角形,
為正三角形, ;(Ⅱ) AB=
;(Ⅱ) AB= .
. 為正三角形,
為正三角形,
 .
. =sin∠AFB=
=sin∠AFB= ,得
,得 =
= ,所以GH=
,所以GH= .
. ,GH=
,GH= ,得DH=
,得DH= .
. =
= ,得x=
,得x= ,所以AB=
,所以AB= .
. ,0,0),D(-1,
,0,0),D(-1, ,0),B(-2,0,x),所以
,0),B(-2,0,x),所以 =(1,-
=(1,- ,0),
,0), =(2,0,-x).
=(2,0,-x). =(0,1,0).
=(0,1,0). =(x1,y1,z1)為平面BFD的法向量,則
=(x1,y1,z1)為平面BFD的法向量,則
 =(
=( ,1,
,1,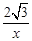 ).因為cos<
).因為cos< ,
, >=
>= =
= ,
, ,所以AB=
,所以AB= .
.

 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案科目:高中數學 來源:不詳 題型:解答題
 ,AF=1,M是線段EF的中點.
,AF=1,M是線段EF的中點.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 中,
中, ,
, ,點
,點 在
在 上,
上, 交
交 于
于 ,
, 交
交 于
于 .沿
.沿 將△
將△ 翻折成△
翻折成△ ,使平面
,使平面 平面
平面 ;沿
;沿 將△
將△ 翻折成△
翻折成△ ,使平面
,使平面 平面
平面 .
.
 平面
平面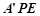 .
. ,當
,當 為何值時,二面角
為何值時,二面角 的大小為
的大小為 ?
?查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
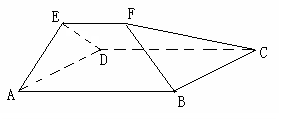
 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 BB1,C1F=
BB1,C1F= CC1.
CC1.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
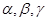 是三個不重合的平面,l是直線,給出下列命題:
是三個不重合的平面,l是直線,給出下列命題: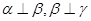 ,則
,則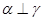 ; ②若
; ②若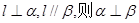
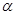 的距離相等,則
的距離相等,則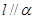 ; ④若
; ④若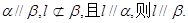
| A.①② | B.②③ | C.②④ | D.③④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com