
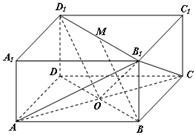
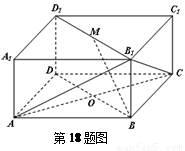
(12分)如圖所示的長方體 中,
中,
底面 是邊長為
是邊長為 的正方形,
的正方形, 為
為 與
與 的交點,
的交點,
 ,
,  是線段
是線段 的中點.
的中點.
(1)求證: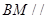 平面
平面 ;
;
(2)求三棱錐 的體積.
的體積.

解:(1)連結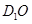 ,如圖,
,如圖,
∵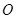 、
、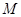 分別是
分別是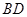 、
、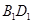 的中點,
的中點, 是矩形,
是矩形,
∴四邊形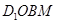 是平行四邊形,
是平行四邊形,
∴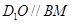 . --------2分
. --------2分
∵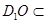 平面
平面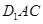 ,
,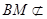 平面
平面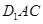 ,
,
∴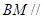 平面
平面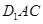 .-------------------6分
.-------------------6分
(2)解法1 連結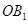 ,∵正方形
,∵正方形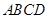 的邊長為2,
的邊長為2,
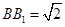 ,∴
,∴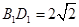 ,
,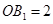 ,
,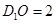 ,則
,則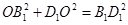 ,
,
∴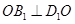 .
--------------------------------------------------------8分
.
--------------------------------------------------------8分
又∵在長方體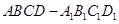 中,
中,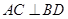 ,
,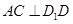 ,且
,且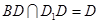 ,
,
∴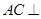 平面
平面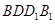 ,又
,又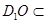 平面
平面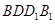 ,[來源:學_科_網]
,[來源:學_科_網]
∴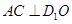 ,又
,又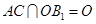 ,
,
∴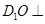 平面
平面 ,即
,即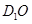 為三棱錐
為三棱錐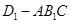 的高.---------10分
的高.---------10分
∵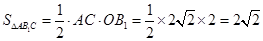 ,
,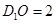
∴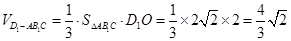 .
--------------------------------12分
.
--------------------------------12分
解法2 三棱錐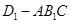 是長方體
是長方體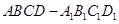 割去三棱錐
割去三棱錐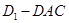 、三棱錐
、三棱錐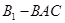 、三棱錐
、三棱錐 、三棱錐
、三棱錐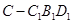 后所得,而三棱錐
后所得,而三棱錐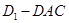 、
、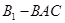 、
、 、
、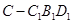 是等底等高,故其體積相等.
是等底等高,故其體積相等.
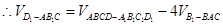
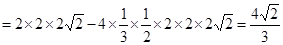 .
.
【解析】略


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2013屆廣東省高二下期末文科數學試卷(解析版) 題型:解答題
(本小題滿分14分)
如圖所示的長方體 中,底面
中,底面 是邊長為
是邊長為 的正方形,
的正方形, 為
為 與
與 的交點,
的交點, ,
,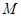 是線段
是線段 的中點.
的中點.

(1)求證: 平面
平面 ;
;
(2)求三棱錐D1-ABC的體積.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省高三第一次月考理科數學卷 題型:解答題
(本小題滿分14分)
如圖所示的長方體 中,底面
中,底面 是邊長為
是邊長為 的正方形,
的正方形,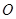 為
為 與
與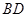 的交點,
的交點, ,
, 是線段
是線段 的中點.
的中點.
(Ⅰ)求證: 平面
平面 ;
;
(Ⅱ)求證: 平面
平面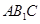 ;
;
(Ⅲ)求二面角 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省高三第一次月考理科數學卷 題型:解答題
(本小題滿分14分)
如圖所示的長方體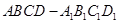 中,底面
中,底面 是邊長為
是邊長為 的正方形,
的正方形,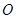 為
為 與
與 的交點,
的交點, ,
,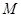 是線段
是線段 的中點.
的中點.
(Ⅰ)求證: 平面
平面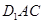 ;
;
(Ⅱ)求證: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com