
已知 是等差數列,首項
是等差數列,首項 ,前
,前 項和為
項和為 .令
.令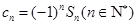 ,
, 的前
的前 項和
項和 .數列
.數列 是公比為
是公比為 的等比數列,前
的等比數列,前 項和為
項和為 ,且
,且 ,
, .
.
(1)求數列 、
、 的通項公式;
的通項公式;
(2)證明: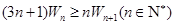 .
.
(1)  ,
, ;(2)見解析.
;(2)見解析.
解析試題分析:(1)首先設等差數列的公差為 ,由已知建立
,由已知建立 的方程,求得
的方程,求得 ,寫出等差數列的通項公式;進一步確定等比數列的公比,求得等比數列的通項公式.
,寫出等差數列的通項公式;進一步確定等比數列的公比,求得等比數列的通項公式.
(2)求得 ,將不等式加以轉化成
,將不等式加以轉化成 ,
,
即證: .注意到這是與自然數有關的不等式證明問題,故考慮應用數學歸納法.
.注意到這是與自然數有關的不等式證明問題,故考慮應用數學歸納法.
很明顯 時,
時, ,因此用數學歸納法證明:當
,因此用數學歸納法證明:當 時,
時, .
.
試題解析:(1)設等差數列的公差為 ,因為
,因為
所以
則
則
解得 ,所以
,所以 4分
4分
所以 ,
,
所以 6分
6分
(2)由(1)知,
要證 ,
,
只需證
即證: 8分
8分
當 時,
時,
下面用數學歸納法證明:當 時,
時,
(1)當 時,左邊
時,左邊 ,右邊
,右邊 ,左
,左 右,不等式成立
右,不等式成立
(2)假設 ,
,
則 時,
時,
 時不等式成立
時不等式成立
根據(1)(2)可知:當 時,
時,
綜上可知: 對于
對于 成立
成立
所以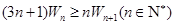 12分
12分
考點:等差數列、等比數列的通項公式及其求和公式,數學歸納法.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:解答題
設數列{an}、{bn}、{cn}滿足:bn=an-an+2,cn=an+2an+1+3an+2(n=1,2,3,…),求證:{an}為等差數列的充分必要條件是{cn}為等差數列且bn≤bn+1(n=1,2,3,…).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(1)已知兩個等比數列{an},{bn},滿足a1=a(a>0),b1-a1=1,b2-a2=2,b3-a3=3,若數列{an}唯一,求a的值;
(2)是否存在兩個等比數列{an},{bn},使得b1-a1,b2-a2,b3-a3,b4-a4成公差不為0的等差數列?若存在,求{an},{bn}的通項公式;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在等差數列{an}中,a1=3,其前n項和為Sn,等比數列{bn}的各項均為正數,b1=1,公比為q,且b2+S2=12,q=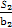 .
.
(1)求an與bn.
(2)證明: ≤
≤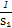 +
+ +…+
+…+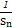 <
< .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
等差數列{an}的首項為a1,公差d=-1,前n項和為Sn.
(1)若S5=-5,求a1的值.
(2)若Sn≤an對任意正整數n均成立,求a1的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設各項均為正數的數列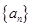 的前
的前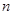 項和為
項和為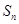 ,滿足
,滿足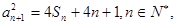 且
且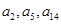 恰好是等比數列
恰好是等比數列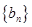 的前三項.
的前三項.
(Ⅰ)求數列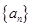 、
、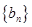 的通項公式;
的通項公式;
(Ⅱ)記數列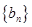 的前
的前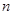 項和為
項和為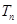 ,若對任意的
,若對任意的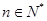 ,
,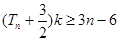 恒成立,求實數
恒成立,求實數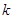 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com