
如圖,四棱錐P-ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45,點(diǎn)E、F分別為棱AB、PD的中點(diǎn).

(1)求證:AF∥平面PCE;
(2)求三棱錐C-BEP的體積.
(1)詳見(jiàn)解析;(2)三棱錐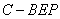 的體積為
的體積為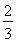 .
.
【解析】
試題分析:(1)求證: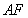 ∥平面
∥平面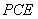 ,證明線面平行,首先證明線線平行,可用三角形的中位線平行,也可用平行四邊形的對(duì)邊平行,本題欲證
,證明線面平行,首先證明線線平行,可用三角形的中位線平行,也可用平行四邊形的對(duì)邊平行,本題欲證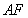 ∥平面
∥平面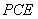 ,根據(jù)直線與平面平行的判定定理可知只需證
,根據(jù)直線與平面平行的判定定理可知只需證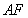 與平面
與平面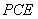 內(nèi)一直線平行,取
內(nèi)一直線平行,取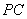 的中點(diǎn)
的中點(diǎn)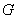 ,連接
,連接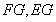 ,易證
,易證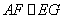 ,從而得
,從而得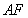 ∥平面
∥平面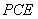 ;(2)求三棱錐
;(2)求三棱錐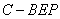 的體積,三棱錐
的體積,三棱錐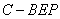 的體積可轉(zhuǎn)化成三棱錐
的體積可轉(zhuǎn)化成三棱錐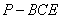 的體積,而
的體積,而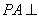 底面
底面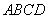 ,從而
,從而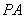 即為三棱錐
即為三棱錐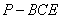 的高,根據(jù)三棱錐的體積公式進(jìn)行求解即可.
的高,根據(jù)三棱錐的體積公式進(jìn)行求解即可.
試題解析:(1)證明:取PC的中點(diǎn)G,連接GF,因?yàn)?/span>F為PD的中點(diǎn),
所以,GF∥CD且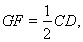 又E為AB的中點(diǎn),ABCD是正方形,
又E為AB的中點(diǎn),ABCD是正方形,
所以,AE∥CD且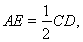 故AE∥GF且
故AE∥GF且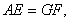
所以,AEGF是平行四邊形,故AF∥EG,而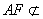 平面
平面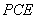 ,
,
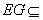 平面
平面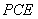 ,所以,AF∥平面
,所以,AF∥平面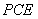 .
.
(2)因?yàn)?/span>PA⊥底面ABCD,所以,PA是三棱錐P-EBC的高,PA⊥AD,PA=2,
∠PDA=450,所以,AD=2,正方形ABCD中,E為AB的中點(diǎn),所以,EB=1,故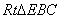 的面積為1,故
的面積為1,故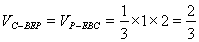 .
.
故三棱錐C-BEP的體積為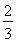 .
.
考點(diǎn):直線與平面平行的判定;棱柱、棱錐、棱臺(tái)的體積.


 開(kāi)心快樂(lè)假期作業(yè)暑假作業(yè)西安出版社系列答案
開(kāi)心快樂(lè)假期作業(yè)暑假作業(yè)西安出版社系列答案 名題訓(xùn)練系列答案
名題訓(xùn)練系列答案 期末集結(jié)號(hào)系列答案
期末集結(jié)號(hào)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:2013-2014學(xué)年高中數(shù)學(xué)人教A版選修4-1知能達(dá)標(biāo)2-1練習(xí)卷(解析版) 題型:填空題
如圖所示,AB為⊙O的直徑,AC=4 cm,BC=3 cm,CD⊥AB于D,則CD的長(zhǎng)為________ cm.
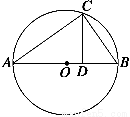
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2013-2014學(xué)年高中數(shù)學(xué)人教A版選修4-1知能達(dá)標(biāo)1-1練習(xí)卷(解析版) 題型:填空題
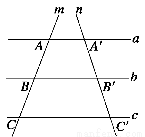
如圖所示,已知a∥b∥c,直線m、n分別與a、b、c交于點(diǎn)A、B、C和A′、B′、C′,如果AB=BC=1,A′B′=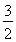 ,則B′C′=________.
,則B′C′=________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2013-2014學(xué)年陜西西安第一中學(xué)高三第二學(xué)期第二次模擬考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:選擇題
設(shè)第一象限內(nèi)的點(diǎn) 滿足約束條件
滿足約束條件 ,若目標(biāo)函數(shù)
,若目標(biāo)函數(shù)
 的最大值為40,則
的最大值為40,則 的最小值為( )
的最小值為( )
(A) (B)
(B) (C)1 (D)4
(C)1 (D)4
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2013-2014學(xué)年陜西西安第一中學(xué)高三第二學(xué)期第二次模擬考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:選擇題
復(fù)數(shù)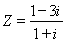 的實(shí)部是 ( )
的實(shí)部是 ( )
A. 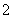 B.
B.  C.
C.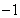 D.
D.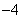
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2013-2014學(xué)年陜西西安第一中學(xué)高三第二學(xué)期第二次模擬考試文科數(shù)學(xué)試卷(解析版) 題型:填空題
若存在實(shí)數(shù)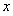 使
使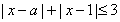 成立,則實(shí)數(shù)
成立,則實(shí)數(shù)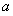 的取值范圍是
的取值范圍是
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2013-2014學(xué)年陜西西安第一中學(xué)高三第二學(xué)期第二次模擬考試文科數(shù)學(xué)試卷(解析版) 題型:選擇題
直線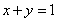 與圓
與圓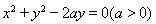 沒(méi)有公共點(diǎn),則
沒(méi)有公共點(diǎn),則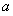 的取值范圍是( )
的取值范圍是( )
A.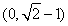 B.
B.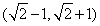 C.
C.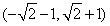 D.
D.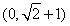
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com