
 的圖象和直線y=x無交點,現有下列結論:
的圖象和直線y=x無交點,現有下列結論: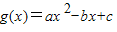 的圖象與直線y=-x也一定沒有交點.
的圖象與直線y=-x也一定沒有交點.

科目:高中數學 來源:2012-2013學年安徽省示范高中高三(上)第一次聯考數學試卷(文科)(解析版) 題型:填空題
 的圖象和直線y=x無交點,現有下列結論:
的圖象和直線y=x無交點,現有下列結論: 的圖象與直線y=-x也一定沒有交點.
的圖象與直線y=-x也一定沒有交點.查看答案和解析>>
科目:高中數學 來源:2012-2013學年安徽省示范高中高三(上)第一次聯考數學試卷(理科)(解析版) 題型:填空題
 的圖象和直線y=x無交點,現有下列結論:
的圖象和直線y=x無交點,現有下列結論: 的圖象與直線y=-x也一定沒有交點.
的圖象與直線y=-x也一定沒有交點.查看答案和解析>>
科目:高中數學 來源:2012-2013學年安徽省示范高中高三(上)第一次聯考數學試卷(文科)(解析版) 題型:填空題
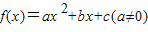 的圖象和直線y=x無交點,現有下列結論:
的圖象和直線y=x無交點,現有下列結論: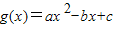 的圖象與直線y=-x也一定沒有交點.
的圖象與直線y=-x也一定沒有交點.查看答案和解析>>
科目:高中數學 來源: 題型:
若二次函數![]() 的圖象和直線y=x無交點,現有下列結論:
的圖象和直線y=x無交點,現有下列結論:
①方程![]() 一定沒有實數根;
一定沒有實數根;
②若a>0,則不等式![]() 對一切實數x都成立;
對一切實數x都成立;
③若a<0,則必存在實數![]() ,使
,使![]() ;
;
④函數![]() 的圖象與直線y=-x一定沒有交點,
的圖象與直線y=-x一定沒有交點,
其中正確的結論是____________(寫出所有正確結論的編號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com