中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

在銳角中，且.
（1）求的大小；
（2）若，求的值.
（1）；（2）若，則的值不存在．

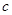
試題分析：（1）求的大小，求角的大小，可用正弦定理來求，也可利用余弦定理來求，本題由已知且，即，符合利用正弦定理來求，故由正弦定理得，利用三角形為銳角三角形，即可求出角的值；（2）若，求的值，由于已知，可利用余弦定理來求邊長，注意，求出后要驗證三角形是否為銳角．
（1）由正弦定理可得                                   2分
因為
所以                             5分
在銳角中，                                      7分
（2）由余弦定理可得                          9分
又因為
所以，即                    11分
解得                     12分
經(jīng)檢驗，由可得，不符合題意，
所以舍去.            13分
練習冊系列答案
相關(guān)習題

科目：高中數(shù)學 來源：不詳 題型：解答題

已知函數(shù)．
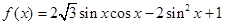
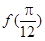
（Ⅰ）求的值；
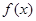
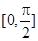
（Ⅱ）求在區(qū)間上的最大值和最小值．

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：解答題

已知向量
m
=（a，b），
n
=（sin2x，2cos2x），若f（x）=
m
•
n
，且f(0)=8，f(
π
6
)=12．
（1）求a，b的值；
（2）求函數(shù)f（x）的最大值及取得最大值時的x的集合；
（3）求函數(shù)f（x）的單調(diào)增區(qū)間．

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：填空題

已知, ,則        。

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：填空題

在△ABC中，設(shè)AD為BC邊上的高，且AD = BC，b，c分別表示角B，C所對的邊長，則的取值范圍是_______ ．

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：解答題

已知向量．
（1）若，且，求角的值；
（2）若，且，求的值．

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：單選題

從原點向圓x2+y2﹣12y+27=0作兩條切線，則該圓夾在兩條切線問的劣弧長為（　　）
A．πB．2πC．4πD．6π

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：單選題

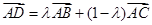
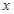
是邊延長線上一點，記. 若關(guān)于的方程
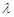
在上恰有兩解，則實數(shù)的取值范圍是（   ）
A．B．或
C．D．或

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：單選題

式子的值為（    ）
A．B．C．D．1

查看答案和解析>>

同步練習冊答案